310501: CF1843C. Sum in Binary Tree
Description
Vanya really likes math. One day when he was solving another math problem, he came up with an interesting tree. This tree is built as follows.
Initially, the tree has only one vertex with the number $1$ — the root of the tree. Then, Vanya adds two children to it, assigning them consecutive numbers — $2$ and $3$, respectively. After that, he will add children to the vertices in increasing order of their numbers, starting from $2$, assigning their children the minimum unused indices. As a result, Vanya will have an infinite tree with the root in the vertex $1$, where each vertex will have exactly two children, and the vertex numbers will be arranged sequentially by layers.
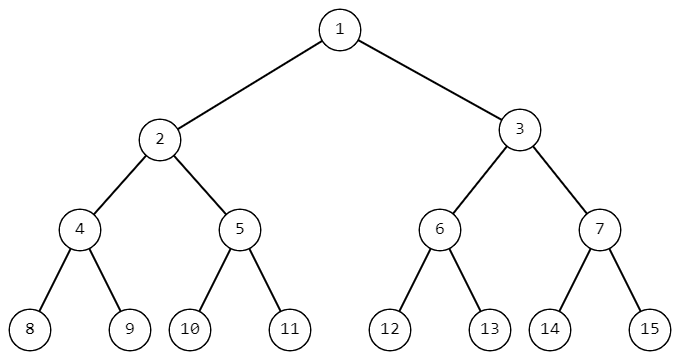Part of Vanya's tree. Vanya wondered what the sum of the vertex numbers on the path from the vertex with number $1$ to the vertex with number $n$ in such a tree is equal to. Since Vanya doesn't like counting, he asked you to help him find this sum.
InputThe first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of test cases.
This is followed by $t$ lines — the description of the test cases. Each line contains one integer $n$ ($1 \le n \le 10^{16}$) — the number of vertex for which Vanya wants to count the sum of vertex numbers on the path from the root to that vertex.
OutputFor each test case, print one integer — the desired sum.
ExampleInput6 3 10 37 1 10000000000000000 15Output
4 18 71 1 19999999999999980 26Note
In the first test case of example on the path from the root to the vertex $3$ there are two vertices $1$ and $3$, their sum equals $4$.
In the second test case of example on the path from the root to the vertex with number $10$ there are vertices $1$, $2$, $5$, $10$, sum of their numbers equals $1+2+5+10 = 18$.
Input
题意翻译
### 简要题意 给定一棵根结点为 $1$ 的完全二叉树，编号为 $x$ 的节点的左儿子编号为 $x$$\times$$2$,右儿子编号为$x$$\times$$2$$+$$1$。从编号为 $1$ 的点到编号为 $n$ 的点的路径上的结点编号之和为多少？Output
Vanya 构建了一棵二叉树，构建规则如下：
1. 初始时，树只有一个顶点，编号为 1，即树的根。
2. 然后给这个根顶点添加两个子顶点，分别赋予连续的编号 2 和 3。
3. 之后，Vanya 按照顶点编号的递增顺序给顶点添加子顶点，从编号 2 开始，给它们的子顶点分配最小的未使用索引。这样，Vanya 将得到一棵以顶点 1 为根的无穷树，其中每个顶点恰好有两个子顶点，且顶点编号按层顺序连续排列。
问题要求计算在这样的树中，从顶点 1 到顶点 n 的路径上顶点编号之和。
**输入数据格式：**
输入的第一行包含一个整数 t（1 ≤ t ≤ 10^4）——测试用例的数量。
接下来 t 行，每行包含一个整数 n（1 ≤ n ≤ 10^16）——Vanya 想要计算从根到该顶点的路径上顶点编号之和的顶点编号。
**输出数据格式：**
对于每个测试用例，输出一个整数——即路径上顶点编号之和。
**示例：**
输入：
```
6
3
10
37
1
10000000000000000
15
```
输出：
```
4
18
71
1
19999999999999980
26
```
**注意：**
- 在第一个测试用例中，从根到顶点 3 的路径上有两个顶点 1 和 3，它们的和等于 4。
- 在第二个测试用例中，从根到编号为 10 的顶点的路径上有顶点 1、2、5、10，它们的编号之和等于 1+2+5+10 = 18。**题目大意：** Vanya 构建了一棵二叉树，构建规则如下： 1. 初始时，树只有一个顶点，编号为 1，即树的根。 2. 然后给这个根顶点添加两个子顶点，分别赋予连续的编号 2 和 3。 3. 之后，Vanya 按照顶点编号的递增顺序给顶点添加子顶点，从编号 2 开始，给它们的子顶点分配最小的未使用索引。这样，Vanya 将得到一棵以顶点 1 为根的无穷树，其中每个顶点恰好有两个子顶点，且顶点编号按层顺序连续排列。 问题要求计算在这样的树中，从顶点 1 到顶点 n 的路径上顶点编号之和。 **输入数据格式：** 输入的第一行包含一个整数 t（1 ≤ t ≤ 10^4）——测试用例的数量。 接下来 t 行，每行包含一个整数 n（1 ≤ n ≤ 10^16）——Vanya 想要计算从根到该顶点的路径上顶点编号之和的顶点编号。 **输出数据格式：** 对于每个测试用例，输出一个整数——即路径上顶点编号之和。 **示例：** 输入： ``` 6 3 10 37 1 10000000000000000 15 ``` 输出： ``` 4 18 71 1 19999999999999980 26 ``` **注意：** - 在第一个测试用例中，从根到顶点 3 的路径上有两个顶点 1 和 3，它们的和等于 4。 - 在第二个测试用例中，从根到编号为 10 的顶点的路径上有顶点 1、2、5、10，它们的编号之和等于 1+2+5+10 = 18。