310513: CF1844G. Tree Weights
Description
You are given a tree with $n$ nodes labelled $1,2,\dots,n$. The $i$-th edge connects nodes $u_i$ and $v_i$ and has an unknown positive integer weight $w_i$. To help you figure out these weights, you are also given the distance $d_i$ between the nodes $i$ and $i+1$ for all $1 \le i \le n-1$ (the sum of the weights of the edges on the simple path between the nodes $i$ and $i+1$ in the tree).
Find the weight of each edge. If there are multiple solutions, print any of them. If there are no weights $w_i$ consistent with the information, print a single integer $-1$.
InputThe first line contains a single integer $n$ ($2 \le n \le 10^5$).
The $i$-th of the next $n-1$ lines contains two integers $u_i$ and $v_i$ ($1 \le u_i,v_i \le n$, $u_i \ne v_i$).
The last line contains $n-1$ integers $d_1,\dots,d_{n-1}$ ($1 \le d_i \le 10^{12}$).
It is guaranteed that the given edges form a tree.
OutputIf there is no solution, print a single integer $-1$. Otherwise, output $n-1$ lines containing the weights $w_1,\dots,w_{n-1}$.
If there are multiple solutions, print any of them.
ExamplesInput5 1 2 1 3 2 4 2 5 31 41 59 26Output
31 10 18 8Input
3 1 2 1 3 18 18Output
-1Input
9 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 2 236 205 72 125 178 216 214 117Output
31 41 59 26 53 58 97 93Note
In the first sample, the tree is as follows:
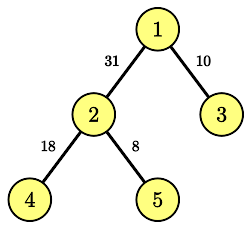
In the second sample, note that $w_2$ is not allowed to be $0$ because it must be a positive integer, so there is no solution.
In the third sample, the tree is as follows:
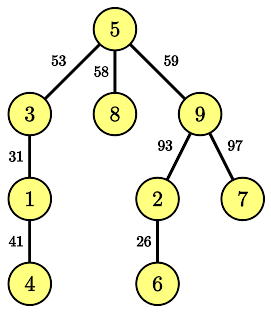
Input
题意翻译
给你一棵节点编号为 $1 \sim n$($2 \le n \le 10^5$) 的无根树,每条边有一条未知的边权。 现在对于所有的 $1 \le i < n$,给出点 $i$ 到点 $i + 1$ 的距离 $d_i$($1 \le d_i \le 10^{12}$),请你还原出任意一组合法的边权或输出 $-1$ 报告无解。Output
输入数据格式:
- 第一行包含一个整数n(2≤n≤10^5)。
- 接下来的n-1行,每行包含两个整数ui和vi(1≤ui,vi≤n,ui≠vi)。
- 最后一行包含n-1个整数d1,...,dn-1(1≤di≤10^12)。
- 保证给定的边构成一棵树。
输出数据格式:
- 如果没有解,输出一个整数-1。
- 否则,输出n-1行,每行包含权重w1,...,wn-1。
- 如果有多个解,输出其中任意一个。
示例输入输出已经给出,用于说明可能的输入和输出情况。题目大意:给定一棵有n个节点的树,节点编号为1,2,...,n。每条边连接两个节点ui和vi,并有一个未知的正整数权重wi。为了帮助你找出这些权重,同时给出了节点i和i+1之间的距离di对于所有1≤i≤n-1(即树中节点i和i+1之间的简单路径上边的权重之和)。找出每条边的权重。如果有多个解,输出其中任意一个。如果没有权重wi与信息一致,则输出-1。 输入数据格式: - 第一行包含一个整数n(2≤n≤10^5)。 - 接下来的n-1行,每行包含两个整数ui和vi(1≤ui,vi≤n,ui≠vi)。 - 最后一行包含n-1个整数d1,...,dn-1(1≤di≤10^12)。 - 保证给定的边构成一棵树。 输出数据格式: - 如果没有解,输出一个整数-1。 - 否则,输出n-1行,每行包含权重w1,...,wn-1。 - 如果有多个解,输出其中任意一个。 示例输入输出已经给出,用于说明可能的输入和输出情况。