310525: CF1846E1. Rudolf and Snowflakes (simple version)

Memory Limit：256 MB Time Limit：2 S
Judge Style：Text Compare Creator：
Submit：0 Solved：0

Description

E1. Rudolf and Snowflakes (simple version)time limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

This is a simple version of the problem. The only difference is that in this version $n \le 10^6$.

One winter morning, Rudolf was looking thoughtfully out the window, watching the falling snowflakes. He quickly noticed a certain symmetry in the configuration of the snowflakes. And like a true mathematician, Rudolf came up with a mathematical model of a snowflake.

He defined a snowflake as an undirected graph constructed according to the following rules:

  • Initially, the graph has only one vertex.
  • Then, more vertices are added to the graph. The initial vertex is connected by edges to $k$ new vertices ($k > 1$).
  • Each vertex that is connected to only one other vertex is connected by edges to $k$ more new vertices. This step should be done at least once.

The smallest possible snowflake for $k = 4$ is shown in the figure.

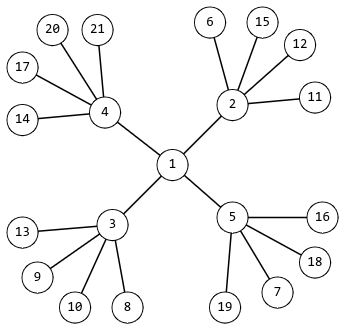
After some mathematical research, Rudolf realized that such snowflakes may not have any number of vertices. Help Rudolf check if a snowflake with $n$ vertices can exist.

Input

The first line of the input contains an integer $t$ ($1 \le t \le 10^4$) — the number of test cases.

Then follow the descriptions of the test cases.

The first line of each test case contains an integer $n$ ($1 \le n \le 10^6$) — the number of vertices for which it is necessary to check the existence of a snowflake.

Output

Output $t$ lines, each of which is the answer to the corresponding test case — "YES" if there exists such $k > 1$ for which a snowflake with the given number of vertices can be constructed; "NO" otherwise.

ExampleInput
9
1
2
3
6
13
15
255
10101
1000000
Output
NO
NO
NO
NO
YES
YES
YES
YES
NO

Input

题意翻译

求是否存在 $n$ 个节点的满 $k$ 叉树，其中 $k ≠ 1$

Output

题目大意：
这是一个关于构建特定类型雪花的问题。在这个简化版本中，需要判断是否可以构建一个具有n个顶点的雪花，其中n≤10^6。雪花由一个无向图构成，构建规则如下：
1. 图最初只有一个顶点。
2. 然后向图中添加更多顶点。初始顶点与k个新顶点相连（k>1）。
3. 每个只连接一个顶点的顶点都会与k个新顶点相连。这一步骤至少执行一次。

输入输出数据格式：
输入：
- 第一行包含一个整数t（1≤t≤10^4），表示测试用例的数量。
- 接下来是t个测试用例的描述，每个测试用例包含一个整数n（1≤n≤10^6），表示需要检查是否存在一个具有n个顶点的雪花。

输出：
- 输出t行，每行对应一个测试用例的答案。如果存在一个k>1，使得可以构建具有给定顶点数的雪花，则输出"YES"；否则输出"NO"。题目大意： 这是一个关于构建特定类型雪花的问题。在这个简化版本中，需要判断是否可以构建一个具有n个顶点的雪花，其中n≤10^6。雪花由一个无向图构成，构建规则如下： 1. 图最初只有一个顶点。 2. 然后向图中添加更多顶点。初始顶点与k个新顶点相连（k>1）。 3. 每个只连接一个顶点的顶点都会与k个新顶点相连。这一步骤至少执行一次。 输入输出数据格式： 输入： - 第一行包含一个整数t（1≤t≤10^4），表示测试用例的数量。 - 接下来是t个测试用例的描述，每个测试用例包含一个整数n（1≤n≤10^6），表示需要检查是否存在一个具有n个顶点的雪花。 输出： - 输出t行，每行对应一个测试用例的答案。如果存在一个k>1，使得可以构建具有给定顶点数的雪花，则输出"YES"；否则输出"NO"。

Source/Category

加入题单

上一题 下一题 算法标签：