310878: CF1903F. Babysitting
Description
Theofanis wants to play video games, however he should also take care of his sister. Since Theofanis is a CS major, he found a way to do both. He will install some cameras in his house in order to make sure his sister is okay.
His house is an undirected graph with $n$ nodes and $m$ edges. His sister likes to play at the edges of the graph, so he has to install a camera to at least one endpoint of every edge of the graph. Theofanis wants to find a vertex cover that maximizes the minimum difference between indices of the chosen nodes.
More formally, let $a_1, a_2, \ldots, a_k$ be a vertex cover of the graph. Let the minimum difference between indices of the chosen nodes be the minimum $\lvert a_i - a_j \rvert$ (where $i \neq j$) out of the nodes that you chose. If $k = 1$ then we assume that the minimum difference between indices of the chosen nodes is $n$.
Can you find the maximum possible minimum difference between indices of the chosen nodes over all vertex covers?
InputThe first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of test cases.
The first line of each test case contains two integers $n$ and $m$ ($1 \le n \le 10^{5}, 1 \le m \le 2 \cdot 10^{5}$) — the number of nodes and the number of edges.
The $i$-th of the following $m$ lines in the test case contains two positive integers $u_i$ and $v_i$ ($1 \le u_i,v_i \le n$), meaning that there exists an edge between them in the graph.
It is guaranteed that the sum of $n$ over all test cases does not exceed $10^{5}$.
It is guaranteed that the sum of $m$ over all test cases does not exceed $2 \cdot 10^{5}$.
OutputFor each test case, print the maximum minimum difference between indices of the chosen nodes over all vertex covers.
ExampleInput3 7 6 1 2 1 3 1 4 1 6 2 3 5 7 3 3 1 2 1 3 1 1 2 4 1 2 1 2 2 1 1 1Output
2 3 2Note
In the first test case, we can install cameras at nodes $1$, $3$, and $7$, so the answer is $2$.
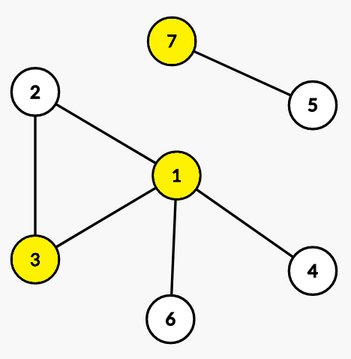
In the second test case, we can install only one camera at node $1$, so the answer is $3$.
Output
Theofanis想要玩视频游戏,但他同时还需要照顾他的妹妹。作为计算机科学专业的学生,他想出了一个既能玩又能照顾妹妹的方法:他在家里安装摄像头,以确保他的妹妹安全。他的房子是一个有n个节点和m条边的无向图,他的妹妹喜欢在图的边缘玩耍,所以他必须至少在每个边的端点之一安装一个摄像头。Theofanis想要找到一个顶点覆盖,使得所选节点的索引之间的最小差异最大化。更正式地说,设a1, a2, …, ak是该图的一个顶点覆盖。设所选节点的索引之间的最小差异为最小的|ai - aj|(其中i ≠ j)。如果k = 1,则我们假设所选节点的索引之间的最小差异是n。你能找到所有顶点覆盖中,所选节点的索引之间的最大可能最小差异吗?
输入输出数据格式:
输入:
- 第一行包含一个整数t(1≤t≤10^4)——测试用例的数量。
- 每个测试用例的第一行包含两个整数n和m(1≤n≤10^5,1≤m≤2×10^5)——节点的数量和边的数量。
- 接下来的m行,每行包含两个正整数ui和vi(1≤ui,vi≤n),表示图中存在一条边连接它们。
- 保证所有测试用例的n之和不超过10^5。
- 保证所有测试用例的m之和不超过2×10^5。
输出:
- 对于每个测试用例,打印所有顶点覆盖中,所选节点的索引之间的最大可能最小差异。
示例:
输入:
```
3
7 6
1 2
1 3
1 4
1 6
2 3
5 7
3 3
1 2
1 3
1 1
2 4
1 2
1 2
2 1
1 1
```
输出:
```
2
3
2
```
注意:
- 在第一个测试用例中,我们可以在节点1、3和7安装摄像头,所以答案是2。
- 在第二个测试用例中,我们只能在节点1安装一个摄像头,所以答案是3。题目大意: Theofanis想要玩视频游戏,但他同时还需要照顾他的妹妹。作为计算机科学专业的学生,他想出了一个既能玩又能照顾妹妹的方法:他在家里安装摄像头,以确保他的妹妹安全。他的房子是一个有n个节点和m条边的无向图,他的妹妹喜欢在图的边缘玩耍,所以他必须至少在每个边的端点之一安装一个摄像头。Theofanis想要找到一个顶点覆盖,使得所选节点的索引之间的最小差异最大化。更正式地说,设a1, a2, …, ak是该图的一个顶点覆盖。设所选节点的索引之间的最小差异为最小的|ai - aj|(其中i ≠ j)。如果k = 1,则我们假设所选节点的索引之间的最小差异是n。你能找到所有顶点覆盖中,所选节点的索引之间的最大可能最小差异吗? 输入输出数据格式: 输入: - 第一行包含一个整数t(1≤t≤10^4)——测试用例的数量。 - 每个测试用例的第一行包含两个整数n和m(1≤n≤10^5,1≤m≤2×10^5)——节点的数量和边的数量。 - 接下来的m行,每行包含两个正整数ui和vi(1≤ui,vi≤n),表示图中存在一条边连接它们。 - 保证所有测试用例的n之和不超过10^5。 - 保证所有测试用例的m之和不超过2×10^5。 输出: - 对于每个测试用例,打印所有顶点覆盖中,所选节点的索引之间的最大可能最小差异。 示例: 输入: ``` 3 7 6 1 2 1 3 1 4 1 6 2 3 5 7 3 3 1 2 1 3 1 1 2 4 1 2 1 2 2 1 1 1 ``` 输出: ``` 2 3 2 ``` 注意: - 在第一个测试用例中,我们可以在节点1、3和7安装摄像头,所以答案是2。 - 在第二个测试用例中,我们只能在节点1安装一个摄像头,所以答案是3。