310890: CF1905E. One-X

E. One-Xtime limit per test3 secondsmemory limit per test512 megabytesinputstandard inputoutputstandard output

In this sad world full of imperfections, ugly segment trees exist.

A segment tree is a tree where each node represents a segment and has its number. A segment tree for an array of $n$ elements can be built in a recursive manner. Let's say function $\operatorname{build}(v,l,r)$ builds the segment tree rooted in the node with number $v$ and it corresponds to the segment $[l,r]$.

Now let's define $\operatorname{build}(v,l,r)$:

• If $l=r$, this node $v$ is a leaf so we stop adding more edges
• Else, we add the edges $(v, 2v)$ and $(v, 2v+1)$. Let $m=\lfloor \frac{l+r}{2} \rfloor$. Then we call $\operatorname{build}(2v,l,m)$ and $\operatorname{build}(2v+1,m+1,r)$.

So, the whole tree is built by calling $\operatorname{build}(1,1,n)$.

Now Ibti will construct a segment tree for an array with $n$ elements. He wants to find the sum of $\operatorname{lca}^\dagger(S)$, where $S$ is a non-empty subset of leaves. Notice that there are exactly $2^n - 1$ possible subsets. Since this sum can be very large, output it modulo $998\,244\,353$.

$^\dagger\operatorname{lca}(S)$ is the number of the least common ancestor for the nodes that are in $S$.

Input

Each test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^3$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ($2 \le n \le 10^{18}$) — the length of the array for which the segment tree is built.

Output

For each test case, output a single integer — the required sum modulo $998\,244\,353$.

ExampleInput

5
2
3
4
5
53278

Output

6
17
36
69
593324855

Note

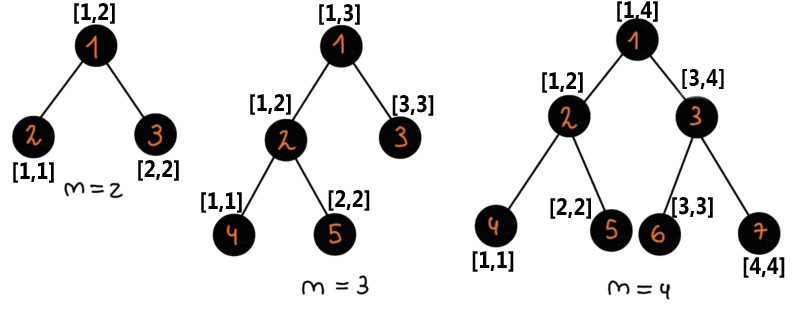
In the first test case:

Let's look at all subsets of leaves.

• $\operatorname{lca}(\{2\})=2$;
• $\operatorname{lca}(\{3\})=3$;
• $\operatorname{lca}(\{2,3\})=1$.

Thus, the answer is $2+3+1=6$.

In the second test case:

Let's look at all subsets of leaves.

• $\operatorname{lca}(\{4\})=4$;
• $\operatorname{lca}(\{5\})=5$;
• $\operatorname{lca}(\{3\})=3$;
• $\operatorname{lca}(\{4,5\})=2$;
• $\operatorname{lca}(\{4,3\})=1$;
• $\operatorname{lca}(\{5,3\})=1$;
• $\operatorname{lca}(\{4,5,3\})=1$;

Thus, the answer is $4+5+3+2+1+1+1=17$.

题目大意：
这个题目是关于线段树的。线段树是一种每个节点代表一个线段并具有其编号的树。一个有n个元素的数组的线段树可以用递归的方式构建。定义一个函数build(v, l, r)来构建以编号为v的节点为根的线段树，它对应于线段[l, r]。

当l=r时，节点v是叶子节点，停止添加边；
否则，添加边(v, 2v)和(v, 2v+1)。令m=⌊(l+r)/2⌋。然后调用build(2v, l, m)和build(2v+1, m+1, r)。
所以，通过调用build(1,1,n)来构建整棵树。

现在Ibti要为一个有n个元素的数组构建线段树。他想要找到sum of lca†(S)，其中S是叶节点的非空子集。注意，恰好有2^n - 1个可能的子集。由于这个和可能非常大，所以输出它模998,244,353的结果。

†lca(S)是S中节点的最小公共祖先的编号。

输入输出数据格式：
输入：
第一行包含一个整数t(1≤t≤10^3)——测试用例的数量。
每个测试用例的第一行包含一个整数n(2≤n≤10^18)——构建线段树的数组的长度。

输出：
对于每个测试用例，输出一个整数——所需和模998,244,353的结果。题目大意： 这个题目是关于线段树的。线段树是一种每个节点代表一个线段并具有其编号的树。一个有n个元素的数组的线段树可以用递归的方式构建。定义一个函数build(v, l, r)来构建以编号为v的节点为根的线段树，它对应于线段[l, r]。 当l=r时，节点v是叶子节点，停止添加边； 否则，添加边(v, 2v)和(v, 2v+1)。令m=⌊(l+r)/2⌋。然后调用build(2v, l, m)和build(2v+1, m+1, r)。 所以，通过调用build(1,1,n)来构建整棵树。 现在Ibti要为一个有n个元素的数组构建线段树。他想要找到sum of lca†(S)，其中S是叶节点的非空子集。注意，恰好有2^n - 1个可能的子集。由于这个和可能非常大，所以输出它模998,244,353的结果。 †lca(S)是S中节点的最小公共祖先的编号。 输入输出数据格式： 输入： 第一行包含一个整数t(1≤t≤10^3)——测试用例的数量。 每个测试用例的第一行包含一个整数n(2≤n≤10^18)——构建线段树的数组的长度。 输出： 对于每个测试用例，输出一个整数——所需和模998,244,353的结果。