311011: CF1920F2. Smooth Sailing (Hard Version)

F2. Smooth Sailing (Hard Version)time limit per test5 secondsmemory limit per test1024 megabytesinputstandard inputoutputstandard output

The only difference between the two versions of this problem is the constraint on $q$. You can make hacks only if both versions of the problem are solved.

Thomas is sailing around an island surrounded by the ocean. The ocean and island can be represented by a grid with $n$ rows and $m$ columns. The rows are numbered from $1$ to $n$ from top to bottom, and the columns are numbered from $1$ to $m$ from left to right. The position of a cell at row $r$ and column $c$ can be represented as $(r, c)$. Below is an example of a valid grid.

Example of a valid grid

There are three types of cells: island, ocean and underwater volcano. Cells representing the island are marked with a '#', cells representing the ocean are marked with a '.', and cells representing an underwater volcano are marked with a 'v'. It is guaranteed that there is at least one island cell and at least one underwater volcano cell. It is also guaranteed that the set of all island cells forms a single connected component$^{\dagger}$ and the set of all ocean cells and underwater volcano cells forms a single connected component. Additionally, it is guaranteed that there are no island cells at the edge of the grid (that is, at row $1$, at row $n$, at column $1$, and at column $m$).

Define a round trip starting from cell $(x, y)$ as a path Thomas takes which satisfies the following conditions:

• The path starts and ends at $(x, y)$.
• If Thomas is at cell $(i, j)$, he can go to cells $(i+1, j)$, $(i-1, j)$, $(i, j-1)$, and $(i, j+1)$ as long as the destination cell is an ocean cell or an underwater volcano cell and is still inside the grid. Note that it is allowed for Thomas to visit the same cell multiple times in the same round trip.
• The path must go around the island and fully encircle it. Some path $p$ fully encircles the island if it is impossible to go from an island cell to a cell on the grid border by only traveling to adjacent on a side or diagonal cells without visiting a cell on path $p$. In the image below, the path starting from $(2, 2)$, going to $(1, 3)$, and going back to $(2, 2)$ the other way does not fully encircle the island and is not considered a round trip.

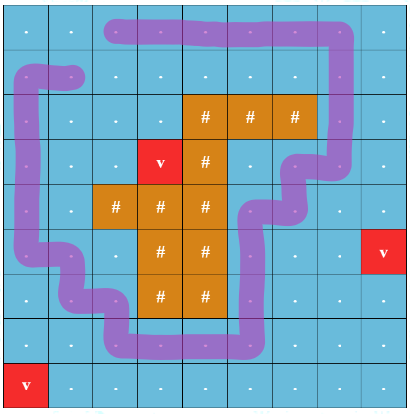Example of a path that does not fully encircle the island

The safety of a round trip is the minimum Manhattan distance$^{\ddagger}$ from a cell on the round trip to an underwater volcano (note that the presence of island cells does not impact this distance).

You have $q$ queries. A query can be represented as $(x, y)$ and for every query, you want to find the maximum safety of a round trip starting from $(x, y)$. It is guaranteed that $(x, y)$ is an ocean cell or an underwater volcano cell.

$^{\dagger}$A set of cells forms a single connected component if from any cell of this set it is possible to reach any other cell of this set by moving only through the cells of this set, each time going to a cell with a common side.

$^{\ddagger}$Manhattan distance between cells $(r_1, c_1)$ and $(r_2, c_2)$ is equal to $|r_1 - r_2| + |c_1 - c_2|$.

Input

The first line contains three integers $n$, $m$, and $q$ ($3 \leq n, m \leq 10^5$, $9 \leq n \cdot m \leq 3 \cdot 10^5$, $1 \leq q \leq 3 \cdot 10^5$) — the number of rows and columns of the grid and the number of queries.

Each of the following $n$ lines contains $m$ characters describing the cells of the grid. The character '#' denotes an island cell, '.' denotes an ocean cell, and 'v' denotes an underwater volcano cell.

It is guaranteed that there is at least one island cell and at least one underwater volcano cell. It is guaranteed that the set of all island cells forms a single connected component and the set of all ocean cells and underwater volcano cells forms a single connected component. Also, it is guaranteed that there are no island cells at the edge of the grid (that is, at the row $1$, at the row $n$, at the column $1$, and at the column $m$).

The following $q$ lines describe the queries. Each of these lines contains two integers $x$ and $y$ ($1 \leq x \leq n$, $1 \leq y \leq m$) denoting a round trip starting from $(x, y)$.

It is guaranteed that $(x, y)$ is an ocean cell or an underwater volcano cell.

Output

For each query, output a single integer — the maximum safety of a round trip starting from the specified position.

ExamplesInput

9 9 3
.........
.........
....###..
...v#....
..###....
...##...v
...##....
.........
v........
1 1
9 1
5 7

Output

3
0
3

Input

3 3 5
..v
.#.
...
1 2
1 3
2 3
2 1
3 2

Output

0
0
0
0
0

Input

14 13 5
.............
.............
.............
...vvvvvvv...
...v.....v...
...v.###.v...
...v.#.#.v...
...v..v..v...
...v..v..v...
....v...v....
.....vvv.....
.............
.............
.............
1 1
7 7
5 6
4 10
13 6

Output

3
0
1
0
2

Input

10 11 4
...........
..#######..
..#..#..#..
..#.....#..
..#..v..#..
..#.###.#..
..#.#.#.#..
..#...#.#..
..#####.#..
...........
7 6
3 7
6 8
1 1

Output

1
2
3
4

Note

For the first example, the image below shows an optimal round trip starting from $(1, 1)$. The round trip has a safety of $3$ as the minimum Manhattan distance from a cell on the round trip to an underwater volcano is $3$.

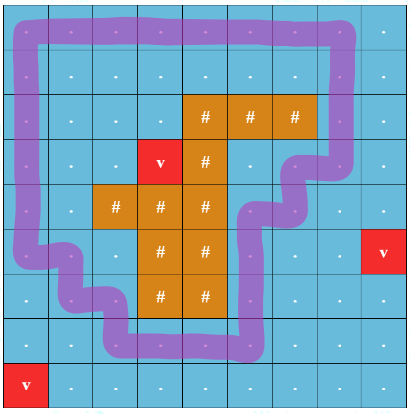Example of an optimal round trip

For the fourth example, remember that it is allowed for Thomas to visit the same cell multiple times in the same round trip. For example, doing so is necessary for the round trip starting from $(7, 6)$.

题目大意：给定一个由海岛、海洋和水下火山组成的网格，要求从给定的海洋或水下火山单元格出发，找到一个环绕海岛的闭环路径，使得路径上的任意海洋或水下火山单元格到最近的水下火山的曼哈顿距离的最大值最大。

输入数据格式：
- 第一行包含三个整数 n、m 和 q（3 ≤ n, m ≤ 10^5，9 ≤ n × m ≤ 3 × 10^5，1 ≤ q ≤ 3 × 10^5），分别表示网格的行数、列数和查询数。
- 接下来 n 行，每行 m 个字符，描述网格的每个单元格。字符 '#' 表示海岛单元格，'.' 表示海洋单元格，'v' 表示水下火山单元格。
- 确保至少有一个海岛单元格和一个水下火山单元格。所有海岛单元格形成一个连通块，所有海洋和水下火山单元格也形成一个连通块。网格边缘没有海岛单元格。
- 接下来 q 行，每行两个整数 x 和 y（1 ≤ x ≤ n，1 ≤ y ≤ m），表示一个从 (x, y) 开始的闭环路径查询。确保 (x, y) 是海洋或水下火山单元格。

输出数据格式：
- 对于每个查询，输出一个整数，表示从指定位置开始的闭环路径的最大安全值。

曼哈顿距离定义：单元格 (r1, c1) 和 (r2, c2) 之间的曼哈顿距离是 |r1 - r2| + |c1 - c2|。

请注意，闭环路径必须环绕海岛，并且路径上的每个海洋或水下火山单元格到最近的水下火山的曼哈顿距离中的最小值决定了路径的安全值。题目大意：给定一个由海岛、海洋和水下火山组成的网格，要求从给定的海洋或水下火山单元格出发，找到一个环绕海岛的闭环路径，使得路径上的任意海洋或水下火山单元格到最近的水下火山的曼哈顿距离的最大值最大。 输入数据格式： - 第一行包含三个整数 n、m 和 q（3 ≤ n, m ≤ 10^5，9 ≤ n × m ≤ 3 × 10^5，1 ≤ q ≤ 3 × 10^5），分别表示网格的行数、列数和查询数。 - 接下来 n 行，每行 m 个字符，描述网格的每个单元格。字符 '#' 表示海岛单元格，'.' 表示海洋单元格，'v' 表示水下火山单元格。 - 确保至少有一个海岛单元格和一个水下火山单元格。所有海岛单元格形成一个连通块，所有海洋和水下火山单元格也形成一个连通块。网格边缘没有海岛单元格。 - 接下来 q 行，每行两个整数 x 和 y（1 ≤ x ≤ n，1 ≤ y ≤ m），表示一个从 (x, y) 开始的闭环路径查询。确保 (x, y) 是海洋或水下火山单元格。 输出数据格式： - 对于每个查询，输出一个整数，表示从指定位置开始的闭环路径的最大安全值。 曼哈顿距离定义：单元格 (r1, c1) 和 (r2, c2) 之间的曼哈顿距离是 |r1 - r2| + |c1 - c2|。 请注意，闭环路径必须环绕海岛，并且路径上的每个海洋或水下火山单元格到最近的水下火山的曼哈顿距离中的最小值决定了路径的安全值。