311018: CF1921G. Mischievous Shooter

Memory Limit：256 MB Time Limit：2 S
Judge Style：Text Compare Creator：
Submit：0 Solved：0

Description

G. Mischievous Shootertime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Once the mischievous and wayward shooter named Shel found himself on a rectangular field of size $n \times m$, divided into unit squares. Each cell either contains a target or not.

Shel only had a lucky shotgun with him, with which he can shoot in one of the four directions: right-down, left-down, left-up, or right-up. When fired, the shotgun hits all targets in the chosen direction, the Manhattan distance to which does not exceed a fixed constant $k$. The Manhattan distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is equal to $|x_1 - x_2| + |y_1 - y_2|$.

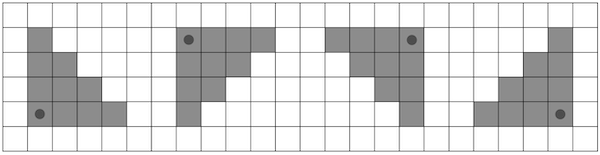Possible hit areas for $k = 3$.

Shel's goal is to hit as many targets as possible. Please help him find this value.

Input

Each test consists of several test cases. The first line contains a single integer $t$ ($1 \le t \le 1000$) — the number of test cases. Then follows the description of the test cases.

The first line of each test case contains field dimensions $n$, $m$, and the constant for the shotgun's power $k$ ($1 \le n, m, k \le 10^5, 1 \le n \cdot m \le 10^5$).

Each of the next $n$ lines contains $m$ characters — the description of the next field row, where the character '.' means the cell is empty, and the character '#' indicates the presence of a target.

It is guaranteed that the sum of $n \cdot m$ over all test cases does not exceed $10^5$.

Output

For each test case, output a single integer on a separate line, which is equal to the maximum possible number of hit targets with one shot.

ExampleInput
4
3 3 1
.#.
###
.#.
2 5 3
###..
...##
4 4 2
..##
###.
#..#
####
2 1 3
#
#
Output
3
4
5
2
Note

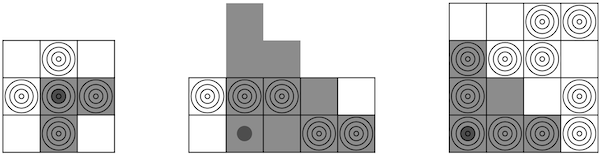
Possible optimal shots for the examples in the statement:

Output

题目大意：
一个名为Shel的淘气射击者发现自己在一个大小为 $ n \times m $ 的矩形区域，该区域被划分为单位正方形，每个单元格要么包含一个目标，要么没有。Shel只有一把幸运的猎枪，他可以用它向四个方向之一射击：右下、左下、左上或右上。当开枪时，猎枪击中选定方向上曼哈顿距离不超过固定常数 $ k $ 的所有目标。两点 $ (x_1, y_1) $ 和 $ (x_2, y_2) $ 之间的曼哈顿距离等于 $ |x_1 - x_2| + |y_1 - y_2| $。Shel的目标是击中尽可能多的目标。请帮助他找到这个值。

输入输出数据格式：
输入：
- 每个测试包含多个测试用例。第一行包含一个整数 $ t $ ($ 1 \le t \le 1000 $) —— 测试用例的数量。接下来是测试用例的描述。
- 每个测试用例的第一行包含字段尺寸 $ n $, $ m $ 和猎枪威力的常数 $ k $ ($ 1 \le n, m, k \le 10^5, 1 \le n \cdot m \le 10^5 $)。
- 接下来的 $ n $ 行每行包含 $ m $ 个字符 —— 下一行字段的描述，其中字符 `.` 表示单元格为空，字符 `#` 表示存在目标。
- 保证所有测试用例的 $ n \cdot m $ 之和不超过 $ 10^5 $。

输出：
- 对于每个测试用例，输出一个单独的整数，该整数等于一次射击可能击中的目标的最大数量。

示例输入输出：
```
Input
4
3 3 1
.#.
###
.#.
2 5 3
###..
...##
4 4 2
..##
###.
#..#
####
2 1 3
#
#

Output
3
4
5
2
```

注意：
题目描述中提到的可能的最优射击方式如下：
[图片描述最优射击方式，图片无法显示]题目大意： 一个名为Shel的淘气射击者发现自己在一个大小为 $ n \times m $ 的矩形区域，该区域被划分为单位正方形，每个单元格要么包含一个目标，要么没有。Shel只有一把幸运的猎枪，他可以用它向四个方向之一射击：右下、左下、左上或右上。当开枪时，猎枪击中选定方向上曼哈顿距离不超过固定常数 $ k $ 的所有目标。两点 $ (x_1, y_1) $ 和 $ (x_2, y_2) $ 之间的曼哈顿距离等于 $ |x_1 - x_2| + |y_1 - y_2| $。Shel的目标是击中尽可能多的目标。请帮助他找到这个值。 输入输出数据格式： 输入： - 每个测试包含多个测试用例。第一行包含一个整数 $ t $ ($ 1 \le t \le 1000 $) —— 测试用例的数量。接下来是测试用例的描述。 - 每个测试用例的第一行包含字段尺寸 $ n $, $ m $ 和猎枪威力的常数 $ k $ ($ 1 \le n, m, k \le 10^5, 1 \le n \cdot m \le 10^5 $)。 - 接下来的 $ n $ 行每行包含 $ m $ 个字符 —— 下一行字段的描述，其中字符 `.` 表示单元格为空，字符 `#` 表示存在目标。 - 保证所有测试用例的 $ n \cdot m $ 之和不超过 $ 10^5 $。 输出： - 对于每个测试用例，输出一个单独的整数，该整数等于一次射击可能击中的目标的最大数量。 示例输入输出： ``` Input 4 3 3 1 .#. ### .#. 2 5 3 ###.. ...## 4 4 2 ..## ###. #..# #### 2 1 3 # # Output 3 4 5 2 ``` 注意： 题目描述中提到的可能的最优射击方式如下： [图片描述最优射击方式，图片无法显示]

Source/Category

加入题单

上一题 下一题 算法标签：