311067: CF1929E. Sasha and the Happy Tree Cutting
Description
Sasha was given a tree$^{\dagger}$ with $n$ vertices as a prize for winning yet another competition. However, upon returning home after celebrating his victory, he noticed that some parts of the tree were missing. Sasha remembers that he colored some of the edges of this tree. He is certain that for any of the $k$ pairs of vertices $(a_1, b_1), \ldots, (a_k, b_k)$, he colored at least one edge on the simple path$^{\ddagger}$ between vertices $a_i$ and $b_i$.
Sasha does not remember how many edges he exactly colored, so he asks you to tell him the minimum number of edges he could have colored to satisfy the above condition.
$^{\dagger}$A tree is an undirected connected graph without cycles.
$^{\ddagger}$A simple path is a path that passes through each vertex at most once.
InputEach test consists of multiple test cases. The first line contains a single integer $t$ ($1 \le t \le 10^4$) — the number of test cases. The description of the test cases follows.
The first line of each test case contains a single integer $n$ ($2 \leq n \leq 10^5$) — the number of vertices in the tree.
The next $(n - 1)$ lines describe the edges of the tree. The $i$-th line contains two integers $u_i$ and $v_i$ ($1 \leq u_i, v_i \leq n$, $u_i \ne v_i$) — the numbers of the vertices connected by the $i$-th edge.
The next line contains a single integer $k$ ($1 \leq k \leq 20$) — the number of pairs of vertices between which Sasha colored at least one edge on a simple path.
The next $k$ lines describe pairs. The $j$-th line contains two integers $a_j$ and $b_j$ ($1 \leq a_j, b_j \leq n, a_j \neq b_j$) — the vertices in the $j$-th pair.
It is guaranteed that the sum of $n$ over all test cases does not exceed $10^5$. It is guaranteed that the sum of $2^k$ over all test cases does not exceed $2^{20}$.
OutputFor each test case, output a single integer — the minimum number of edges Sasha could have colored.
ExampleInput3 4 1 2 2 3 2 4 2 1 3 4 1 6 1 2 3 1 6 1 5 2 4 2 3 3 1 3 6 2 6 5 1 2 2 3 3 4 4 5 4 1 2 2 3 3 4 4 5Output
1 2 4Note
In the first test case, Sasha could have colored only one edge $(1, 2)$. Then, there would be at least one colored edge on the simple path between vertices $1$ and $3$, and vertices $4$ and $1$.
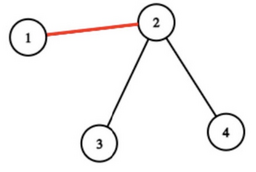
In the second test case, Sasha could have colored the edges $(1, 6)$ and $(1, 3)$.
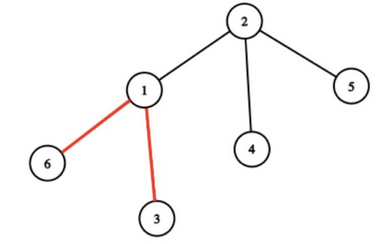
Output
**题目大意**:
萨莎赢得了一场竞赛,奖品是一棵有n个顶点的树。但是,当他回家庆祝胜利时,他注意到树的某些部分不见了。萨莎记得他给这棵树的某些边染了色。他确信对于任意k对顶点(a1, b1), ..., (ak, bk),他在a_i和b_i之间的简单路径上至少染了一条边。
萨莎不记得他确切染了多少条边,所以他要求你告诉他,为了满足上述条件,他可能染的最少边数。
**输入数据格式**:
每个测试包含多个测试用例。第一行包含一个整数t (1 ≤ t ≤ 10^4) — 测试用例的数量。接下来是测试用例的描述。
每个测试用例的第一行包含一个整数n (2 ≤ n ≤ 10^5) — 树中顶点的数量。
接下来的(n - 1)行描述了树的边。第i行包含两个整数u_i和v_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i) — 第i条边连接的两个顶点的编号。
接下来的一行包含一个整数k (1 ≤ k ≤ 20) — 萨莎在简单路径上染了至少一条边的顶点对的数量。
接下来的k行描述了顶点对。第j行包含两个整数a_j和b_j (1 ≤ a_j, b_j ≤ n, a_j ≠ b_j) — 第j对顶点的编号。
保证所有测试用例的n之和不超过10^5。保证所有测试用例的2^k之和不超过2^20。
**输出数据格式**:
对于每个测试用例,输出一个整数 — 萨莎可能染的最少边数。
**示例**:
**输入**:
```
3
4
1 2
2 3
2 4
2
1 3
4 1
6
1 2
3 1
6 1
5 2
4 2
3
3 1
3 6
2 6
5
1 2
2 3
3 4
4 5
4
1 2
2 3
3 4
4 5
```
**输出**:
```
1
2
4
```
**注意**:
- 在第一个测试用例中,萨莎可以只染一条边(1, 2)。这样,在顶点1和3之间以及顶点4和1之间的简单路径上就会至少有一条染色的边。
- 在第二个测试用例中,萨莎可以染边(1, 6)和(1, 3)。**萨莎和快乐的树木切割** **题目大意**: 萨莎赢得了一场竞赛,奖品是一棵有n个顶点的树。但是,当他回家庆祝胜利时,他注意到树的某些部分不见了。萨莎记得他给这棵树的某些边染了色。他确信对于任意k对顶点(a1, b1), ..., (ak, bk),他在a_i和b_i之间的简单路径上至少染了一条边。 萨莎不记得他确切染了多少条边,所以他要求你告诉他,为了满足上述条件,他可能染的最少边数。 **输入数据格式**: 每个测试包含多个测试用例。第一行包含一个整数t (1 ≤ t ≤ 10^4) — 测试用例的数量。接下来是测试用例的描述。 每个测试用例的第一行包含一个整数n (2 ≤ n ≤ 10^5) — 树中顶点的数量。 接下来的(n - 1)行描述了树的边。第i行包含两个整数u_i和v_i (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i) — 第i条边连接的两个顶点的编号。 接下来的一行包含一个整数k (1 ≤ k ≤ 20) — 萨莎在简单路径上染了至少一条边的顶点对的数量。 接下来的k行描述了顶点对。第j行包含两个整数a_j和b_j (1 ≤ a_j, b_j ≤ n, a_j ≠ b_j) — 第j对顶点的编号。 保证所有测试用例的n之和不超过10^5。保证所有测试用例的2^k之和不超过2^20。 **输出数据格式**: 对于每个测试用例,输出一个整数 — 萨莎可能染的最少边数。 **示例**: **输入**: ``` 3 4 1 2 2 3 2 4 2 1 3 4 1 6 1 2 3 1 6 1 5 2 4 2 3 3 1 3 6 2 6 5 1 2 2 3 3 4 4 5 4 1 2 2 3 3 4 4 5 ``` **输出**: ``` 1 2 4 ``` **注意**: - 在第一个测试用例中,萨莎可以只染一条边(1, 2)。这样,在顶点1和3之间以及顶点4和1之间的简单路径上就会至少有一条染色的边。 - 在第二个测试用例中,萨莎可以染边(1, 6)和(1, 3)。