311117: CF1936F. Grand Finale: Circles
Description
You are given $n$ circles on the plane. The $i$-th of these circles is given by a tuple of integers $(x_i, y_i, r_i)$, where $(x_i, y_i)$ are the coordinates of its center, and $r_i$ is the radius of the circle.
Please find a circle $C$ which meets the following conditions:
- $C$ is contained inside all $n$ circles given in the input.
- Among all circles $C$ that meet the first condition, the radius of the circle is maximum.
Let the largest suitable circle have the radius of $a$.
Your output $C$, described as $(x,y,r)$, will be accepted if it meets the following conditions:
- For each $i$, $\sqrt{(x_i-x)^2+(y_i-y)^2}+ r \le r_i+\max(a,1)\cdot 10^{-7}$.
- The absolute or relative error of $r$ does not exceed $10^{-7}$. Formally, your answer is accepted if and only if $\frac{\left|r - a\right|}{\max(1, a)} \le 10^{-7}$.
The first line contains a single integer $n$ ($1 \le n \le 10^5$) — the number of circles.
The $i$-th of the following $n$ lines contains three integers $x_i$, $y_i$, $r_i$ ($-10^6 \le x_i,y_i \le 10^6$, $1 \le r_i \le 2 \cdot 10^6$).
It is guaranteed that there is a circle with a radius of at least $10^{-6}$ which is contained inside all $n$ circles.
OutputOutput three real values, $x$, $y$, and $r$ — the coordinates of the center and the radius of the circle.
ExamplesInput4 1 1 3 -1 1 3 1 -1 2 -1 -1 2Output
0.0000000000000000 -0.7637626158259733 0.9724747683480533Input
4 41580 -23621 95642 -41580 -23621 95642 0 47821 95642 0 0 109750Output
0.0000000000000000 0.0000000000000000 47821.0000000000000000Note
A two-dimensional plot depicting the first test case is given below. The output circle $C$ is dashed with blue lines.
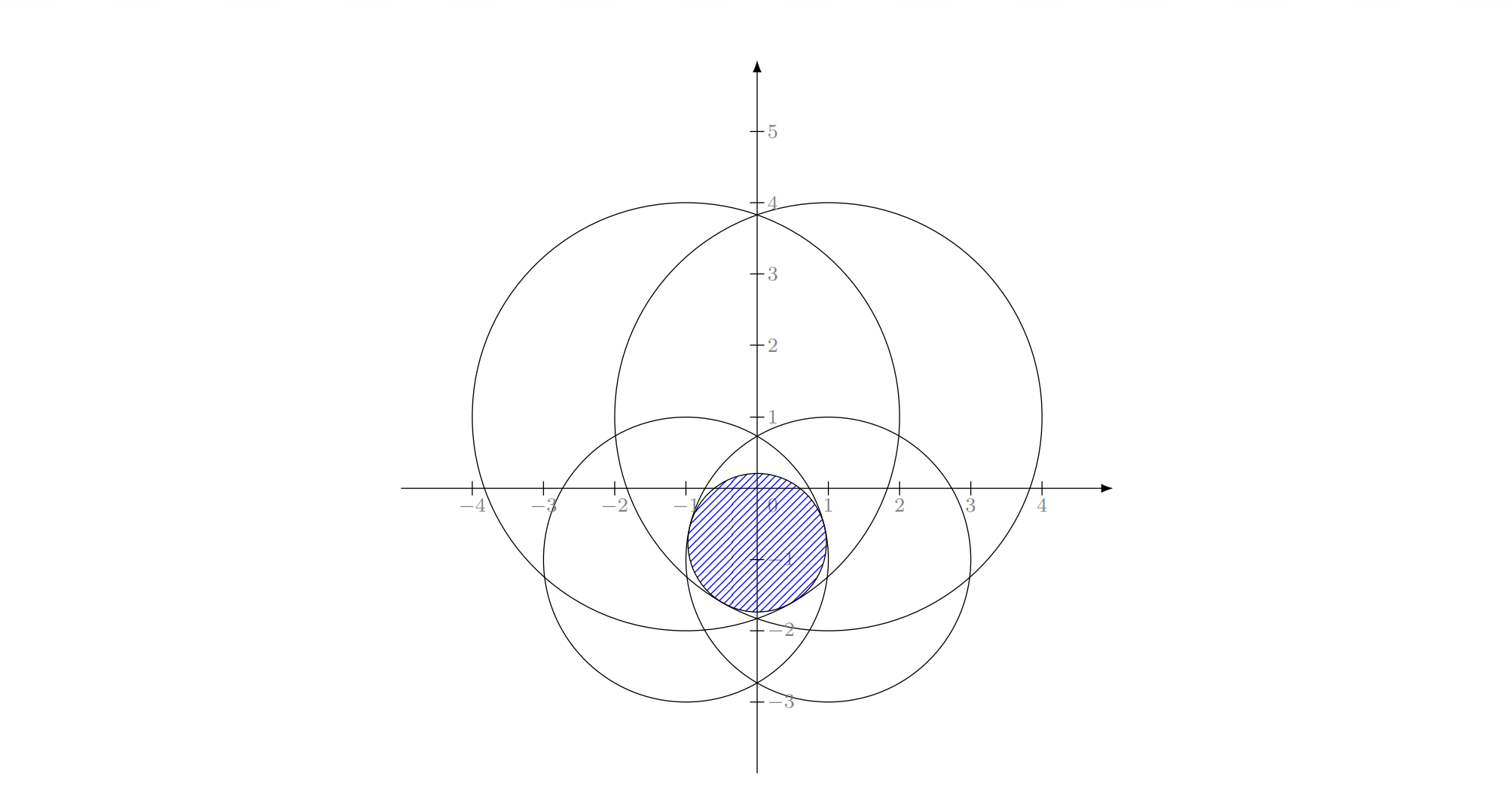
A two-dimensional plot depicting the second test case is given below. The output circle $C$ is dashed with blue lines.
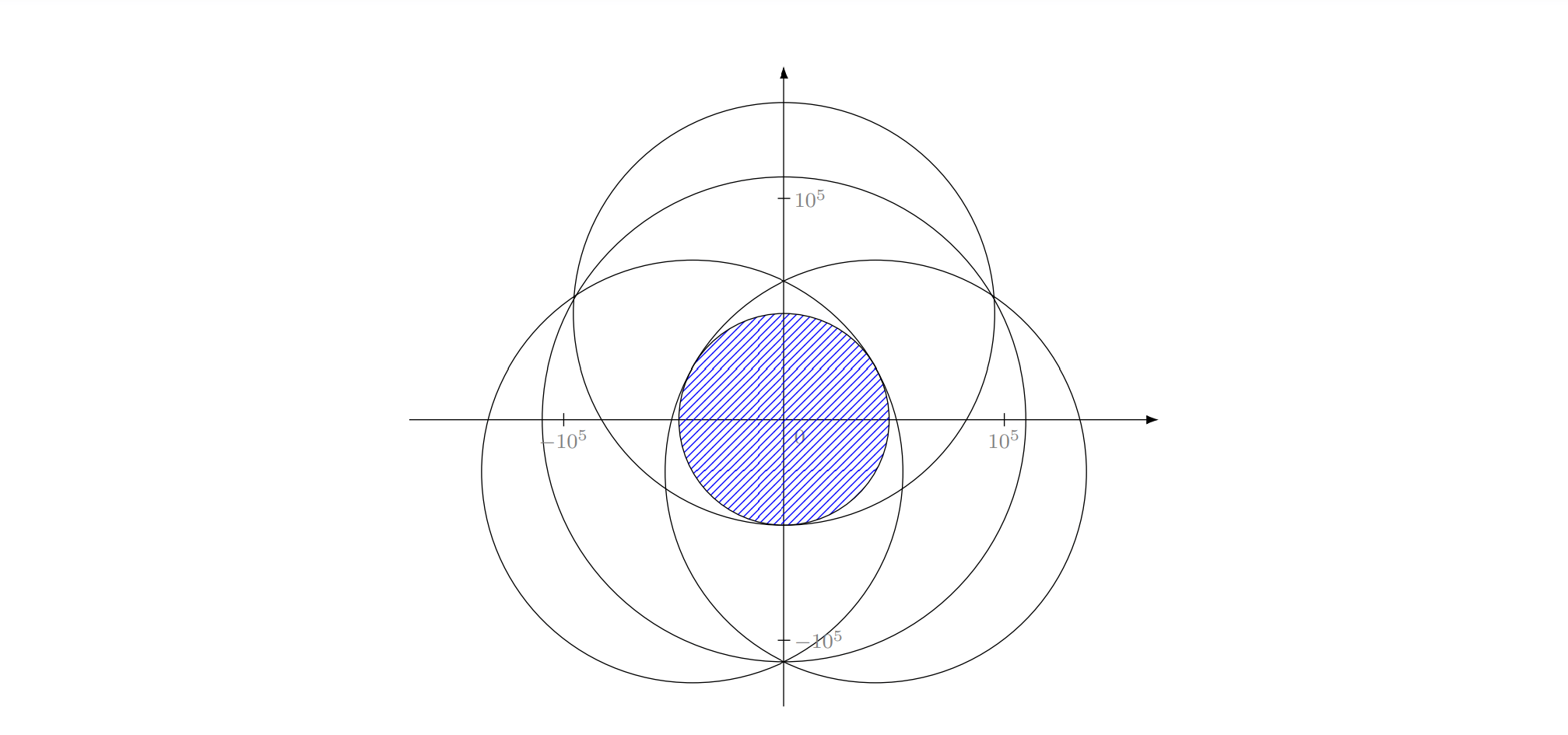
Output
1. C被所有给定的n个圆包含。
2. 在所有满足第一个条件的圆C中,半径最大。
设最大的合适圆的半径为a。你的输出C,用(x,y,r)描述,如果满足以下条件将被接受:
1. 对于每个i,sqrt((x_i-x)^2+(y_i-y)^2) + r <= r_i + max(a,1)*10^-7。
2. r的绝对或相对误差不超过10^-7。正式地,如果|r - a|/max(1, a) <= 10^-7,则你的答案被接受。
输入数据格式:第一行包含一个整数n(1 <= n <= 10^5)——圆的数量。接下来的n行,每行包含三个整数x_i, y_i, r_i(-10^6 <= x_i,y_i <= 10^6,1 <= r_i <= 2 * 10^6)。保证存在一个半径至少为10^-6的圆,该圆被所有n个圆包含。
输出数据格式:输出三个实数值,x, y, r——圆心的坐标和圆的半径。题目大意:给定平面上的n个圆,每个圆由一个三元组(x_i, y_i, r_i)表示,其中(x_i, y_i)是圆心的坐标,r_i是圆的半径。需要找到一个圆C,该圆满足以下条件: 1. C被所有给定的n个圆包含。 2. 在所有满足第一个条件的圆C中,半径最大。 设最大的合适圆的半径为a。你的输出C,用(x,y,r)描述,如果满足以下条件将被接受: 1. 对于每个i,sqrt((x_i-x)^2+(y_i-y)^2) + r <= r_i + max(a,1)*10^-7。 2. r的绝对或相对误差不超过10^-7。正式地,如果|r - a|/max(1, a) <= 10^-7,则你的答案被接受。 输入数据格式:第一行包含一个整数n(1 <= n <= 10^5)——圆的数量。接下来的n行,每行包含三个整数x_i, y_i, r_i(-10^6 <= x_i,y_i <= 10^6,1 <= r_i <= 2 * 10^6)。保证存在一个半径至少为10^-6的圆,该圆被所有n个圆包含。 输出数据格式:输出三个实数值,x, y, r——圆心的坐标和圆的半径。