311151: CF1941G. Rudolf and Subway

Building bridges did not help Bernard, and he continued to be late everywhere. Then Rudolf decided to teach him how to use the subway.

Rudolf depicted the subway map as an undirected connected graph, without self-loops, where the vertices represent stations. There is at most one edge between any pair of vertices.

Two vertices are connected by an edge if it is possible to travel directly between the corresponding stations, bypassing other stations. The subway in the city where Rudolf and Bernard live has a color notation. This means that any edge between stations has a specific color. Edges of a specific color together form a subway line. A subway line cannot contain unconnected edges and forms a connected subgraph of the given subway graph.

An example of the subway map is shown in the figure.

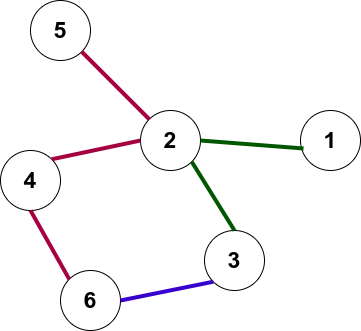
Rudolf claims that the route will be optimal if it passes through the minimum number of subway lines.

Help Bernard determine this minimum number for the given departure and destination stations.

The first line contains an integer $t$ ($1 \le t \le 10^4$) — the number of test cases.

This is followed by descriptions of the test cases.

The first line of each test case contains two integers $n$ and $m$ ($2 \le n \le 2 \cdot 10^5, 1 \le m \le 2 \cdot 10^5$) — the number of subway stations and the number of direct routes between stations (i.e., graph edges).

This is followed by $m$ lines — the description of the edges. Each line of the description contains three integers $u$, $v$, and $c$ ($1 \le u, v \le n, u \ne v, 1 \le c \le 2 \cdot 10^5$) — the numbers of the vertices between which there is an edge, and the color of this edge. It is guaranteed that edges of the same color form a connected subgraph of the given subway graph. There is at most one edge between a pair of any two vertices.

This is followed by two integers $b$ and $e$ ($1 \le b, e \le n$) — the departure and destination stations.

The sum of all $n$ over all test cases does not exceed $2 \cdot 10^5$. The sum of all $m$ over all test cases does not exceed $2 \cdot 10^5$.

For each testcase, output a single integer — the minimum number of subway lines through which the route from station $b$ to station $e$ can pass.

5
6 6
1 2 1
2 3 1
5 2 2
2 4 2
4 6 2
3 6 3
1 3
6 6
1 2 1
2 3 1
5 2 2
2 4 2
4 6 2
3 6 3
1 6
6 6
1 2 1
2 3 1
5 2 2
2 4 2
4 6 2
3 6 3
6 6
4 3
1 2 1
1 3 1
4 1 1
2 3
6 7
1 2 43
1 3 34
4 6 43
6 3 43
2 3 43
5 3 43
4 5 43
1 6

1
2
0
1
1

3
7 9
2 4 1
3 6 1
2 3 5
1 7 1
4 7 1
2 5 4
5 4 4
3 4 1
3 7 1
5 3
6 5
6 5 83691
4 1 83691
5 4 83691
3 2 83691
4 3 83691
5 1
6 7
6 1 83691
6 2 83691
2 5 83691
5 6 83691
2 3 83691
5 4 83574
3 5 83691
1 4

2
1
2

The subway graph for the first example is shown in the figure in the problem statement.

In the first test case, from vertex $1$ to vertex $3$, you can travel along the path $1 \rightarrow 2 \rightarrow 3$, using only the green line.

In the second test case, from vertex $1$ to vertex $6$, you can travel along the path $1 \rightarrow 2 \rightarrow 3 \rightarrow 6$, using the green and blue lines.

In the third test case, there is no need to travel from vertex $6$ to the same vertex, so the number of lines is $0$.

In the fourth test case, all edges of the graph belong to one line, so the answer is $1$.