311155: CF1942C2. Bessie's Birthday Cake (Hard Version)

C2. Bessie's Birthday Cake (Hard Version)time limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard outputProof Geometric Construction Can Solve All Love Affairs - manbo-p⠀

This is the hard version of the problem. The only difference between the two versions is the constraint on $y$. In this version $0 \leq y \leq n - x$. You can make hacks only if both versions are solved.

Bessie has received a birthday cake from her best friend Elsie, and it came in the form of a regular polygon with $n$ sides. The vertices of the cake are numbered from $1$ to $n$ clockwise. You and Bessie are going to choose some of those vertices to cut non-intersecting diagonals into the cake. In other words, the endpoints of the diagonals must be part of the chosen vertices.

Bessie would only like to give out pieces of cake which result in a triangle to keep consistency. The size of the pieces doesn't matter, and the whole cake does not have to be separated into all triangles (other shapes are allowed in the cake, but those will not be counted).

Bessie has already chosen $x$ of those vertices that can be used to form diagonals. She wants you to choose no more than $y$ other vertices such that the number of triangular pieces of cake she can give out is maximized.

What is the maximum number of triangular pieces of cake Bessie can give out?

Input

The first line contains a single integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The first line of each test case consists of three integers, $n$, $x$, and $y$ ($4 \leq n \leq 10^9$, $2 \leq x \leq \min(n, 2 \cdot 10^5)$, $0 \leq y \leq n - x$) — the number of sides of the polygon, number of vertices Bessie has chosen, and the maximum number of other vertices you can choose.

The second line consists of $x$ distinct integers from $1$ to $n$, representing the vertices Bessie has chosen.

It is guaranteed the sum of $x$ over all test cases does not exceed $2 \cdot 10^5$.

Output

For each test case, output a single integer: the maximum number of non-intersecting triangular pieces of cake she can give out.

ExampleInput

3
8 4 2
1 6 2 5
7 3 1
6 4 3
4 2 2
1 3

Output

6
5
2

Note

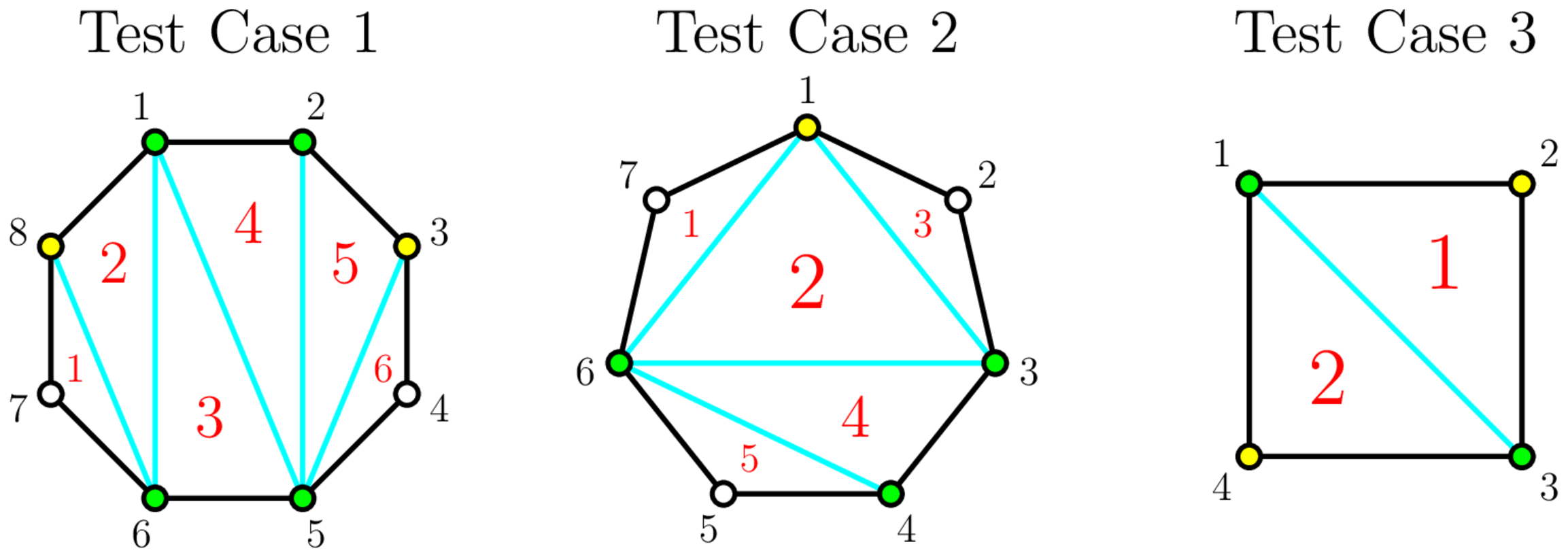
In test cases $1$, $2$ and $3$, you can get $6$, $5$ and $2$ non-intersecting triangular pieces of cake, respectively. A possible construction is shown in the following pictures:

The green dots represent vertices that Bessie chose, the yellow dots represent vertices that you chose, the blue lines represent diagonals that are drawn, and the red numbers represent triangles that are counted.

题目大意：
这是一个难题的版本，与简单版本唯一的不同是对y的限制。在这个版本中，0 ≤ y ≤ n - x。只有当两个版本都解决时，你才能进行hack。

Bessie收到了她的好朋友Elsie送的一个生日蛋糕，这个蛋糕是一个有n边的正多边形。蛋糕的顶点从1到n顺时针编号。你和Bessie将选择一些顶点来切割非交叉的对角线。换句话说，对角线的端点必须是选定的顶点之一。

Bessie只想分发可以形成三角形的蛋糕片以保持一致性。蛋糕片的大小无关紧要，整个蛋糕不必完全分割成所有三角形（蛋糕中允许其他形状，但不会计算在内）。

Bessie已经选择了x个可以用来形成对角线的顶点。她希望您选择不超过y个其他顶点，以便她可以分发的三角形蛋糕片数量最大化。

问：Bessie最多可以分发多少个三角形的蛋糕片？

输入输出数据格式：
输入：
第一行包含一个整数t（1 ≤ t ≤ 10^4）——测试用例的数量。
每个测试用例的第一行包含三个整数n、x和y（4 ≤ n ≤ 10^9，2 ≤ x ≤ min(n, 2 * 10^5)，0 ≤ y ≤ n - x）——多边形的边数、Bessie选择的顶点数以及你可以选择的其他顶点的最大数量。
第二行包含x个从1到n的不同的整数，代表Bessie选择的顶点。
保证所有测试用例中x的总和不超过2 * 10^5。

输出：
对于每个测试用例，输出一个整数：Bessie最多可以分发的非交叉三角形蛋糕片数量。题目大意： 这是一个难题的版本，与简单版本唯一的不同是对y的限制。在这个版本中，0 ≤ y ≤ n - x。只有当两个版本都解决时，你才能进行hack。 Bessie收到了她的好朋友Elsie送的一个生日蛋糕，这个蛋糕是一个有n边的正多边形。蛋糕的顶点从1到n顺时针编号。你和Bessie将选择一些顶点来切割非交叉的对角线。换句话说，对角线的端点必须是选定的顶点之一。 Bessie只想分发可以形成三角形的蛋糕片以保持一致性。蛋糕片的大小无关紧要，整个蛋糕不必完全分割成所有三角形（蛋糕中允许其他形状，但不会计算在内）。 Bessie已经选择了x个可以用来形成对角线的顶点。她希望您选择不超过y个其他顶点，以便她可以分发的三角形蛋糕片数量最大化。 问：Bessie最多可以分发多少个三角形的蛋糕片？ 输入输出数据格式： 输入： 第一行包含一个整数t（1 ≤ t ≤ 10^4）——测试用例的数量。 每个测试用例的第一行包含三个整数n、x和y（4 ≤ n ≤ 10^9，2 ≤ x ≤ min(n, 2 * 10^5)，0 ≤ y ≤ n - x）——多边形的边数、Bessie选择的顶点数以及你可以选择的其他顶点的最大数量。 第二行包含x个从1到n的不同的整数，代表Bessie选择的顶点。 保证所有测试用例中x的总和不超过2 * 10^5。 输出： 对于每个测试用例，输出一个整数：Bessie最多可以分发的非交叉三角形蛋糕片数量。