311197: CF1949A. Grove
Description
You want to plant trees in a square lawn of size $n \times n$ whose corners have Cartesian coordinates $(0, 0)$, $(n, 0)$, $(0, n)$, and $(n, n)$. Trees can only be planted at locations with integer coordinates. Every tree will grow roots within a disk of radius $r$ centered at the location where the tree was planted; such disks must be fully contained in the lawn (possibly touching the boundary of the lawn) and can only intersect each other on their boundaries.
Find a configuration that maximizes the number of trees.
InputThe first and only line contains an integer $n$ ($1 \leq n \leq 20$) and a real number $r$ ($0 < r \leq n/2$) — the length of the sides of the lawn, and the radius of the disks where each tree will grow roots. The real number $r$ is given in decimal notation with at least $1$ and at most $3$ digits after the decimal point.
OutputIn the first line, print the maximum number $m$ of trees that can be planted.
In the next $m$ lines, print a configuration that maximizes the number of trees. Specifically, in the $(i+1)$-th line, print two integers $x$ and $y$ — the coordinates of the location where the $i$-th tree should be planted. You can print the trees in any order.
If there are multiple solutions, print any of them.
ExamplesInput6 1.241Output
2 4 2 2 4Input
9 2.0Output
4 2 2 7 2 2 6 6 6Note
For the first sample, the sample output is shown in the following figure. Note that this is not the only configuration that maximizes the number of trees.
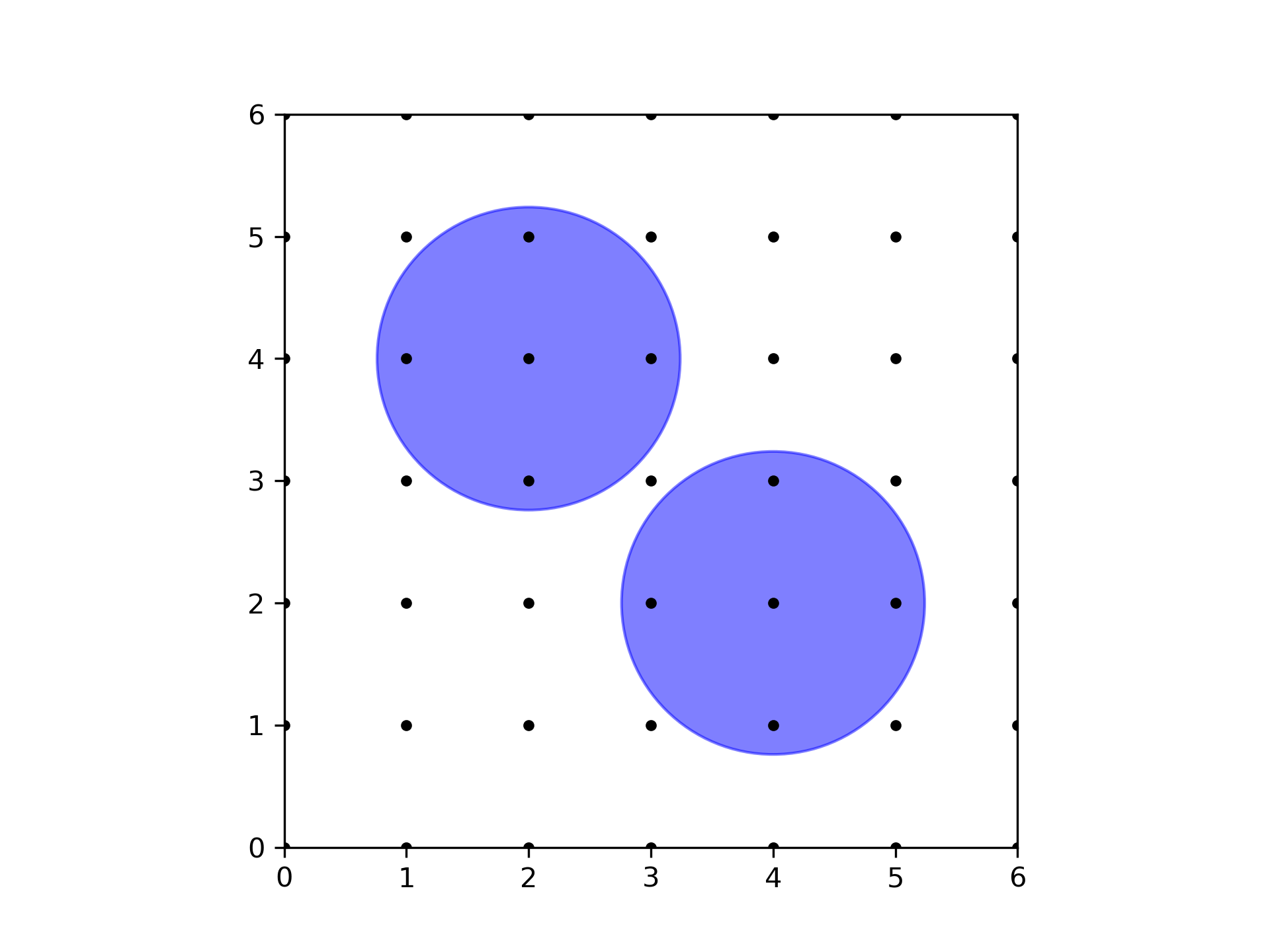
For the second sample, the sample output is shown in the following figure. Note that this is not the only configuration that maximizes the number of trees.
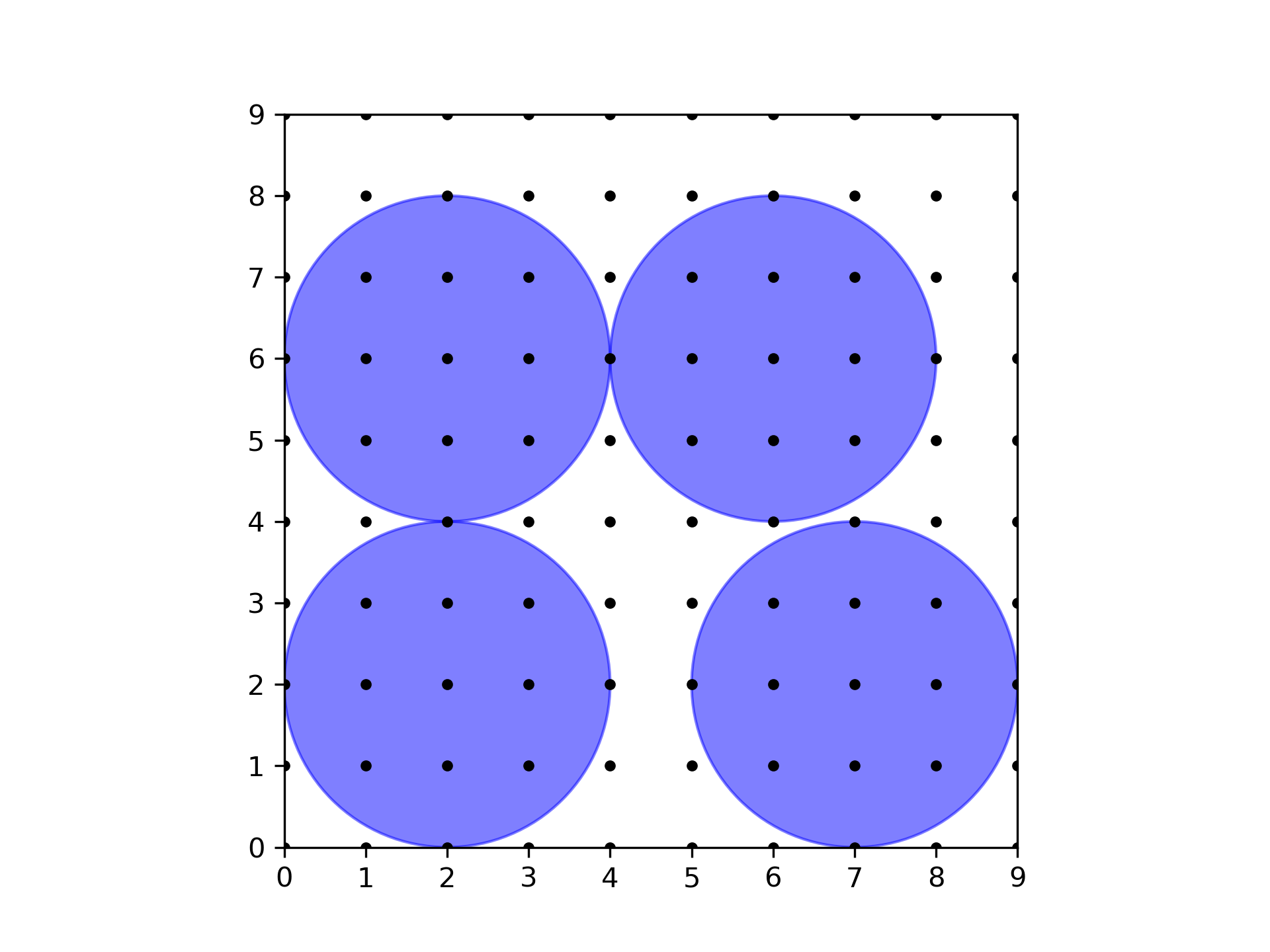
Output
输入数据格式:第一行包含两个数,整数 $ n $ ($ 1 \leq n \leq 20 $) 和实数 $ r $ ($ 0 < r \leq \frac{n}{2} $) —— 草坪的边长和每棵树根系的圆盘半径。实数 $ r $ 以小数形式给出,至少有 1 位小数,最多有 3 位小数。
输出数据格式:第一行打印可以种植的最大树木数目 $ m $。
在接下来的 $ m $ 行中,打印一种最大化树木数量的配置。具体来说,在第 $ (i+1) $ 行中,打印两个整数 $ x $ 和 $ y $ —— 第 $ i $ 棵树应该种植的坐标位置。你可以以任何顺序打印树木。
如果有多个解决方案,打印其中任何一个。题目大意:在一个边长为 $ n \times n $ 的正方形草坪上种植树木,草坪的四个角坐标分别为 $ (0, 0) $, $ (n, 0) $, $ (0, n) $, 和 $ (n, n) $。树木只能在整数坐标点种植,每棵树在其种植点为中心、半径为 $ r $ 的圆盘内生长根系,这些圆盘必须完全位于草坪内(可以接触草坪边界),并且只能在其边界相交。 输入数据格式:第一行包含两个数,整数 $ n $ ($ 1 \leq n \leq 20 $) 和实数 $ r $ ($ 0 < r \leq \frac{n}{2} $) —— 草坪的边长和每棵树根系的圆盘半径。实数 $ r $ 以小数形式给出,至少有 1 位小数,最多有 3 位小数。 输出数据格式:第一行打印可以种植的最大树木数目 $ m $。 在接下来的 $ m $ 行中,打印一种最大化树木数量的配置。具体来说,在第 $ (i+1) $ 行中,打印两个整数 $ x $ 和 $ y $ —— 第 $ i $ 棵树应该种植的坐标位置。你可以以任何顺序打印树木。 如果有多个解决方案,打印其中任何一个。