311205: CF1949I. Disks

I. Diskstime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

You are given $n$ disks in the plane. The center of each disk has integer coordinates, and the radius of each disk is a positive integer. No two disks overlap in a region of positive area, but it is possible for disks to be tangent to each other.

Your task is to determine whether it is possible to change the radii of the disks in such a way that:

• Disks that were tangent to each other remain tangent to each other.
• No two disks overlap in a region of positive area.
• The sum of all radii strictly decreases.

The new radii are allowed to be arbitrary positive real numbers. The centers of the disks cannot be changed.Input

The first line contains an integer $n$ ($1\le n \le 1000$) — the number of disks.

The next $n$ lines contain three integers each. The $i$-th of such lines contains $x_i$, $y_i$ ($-10^9 \leq x_i, y_i \leq 10^9$), and $r_i$ ($1 \leq r_i \leq 10^9$) — the coordinates of the center, and the radius, of the $i$-th disk.

Output

Print $\texttt{YES}$ if it is possible to change the radii in the desired manner. Otherwise, print $\texttt{NO}$.

ExamplesInput

5
0 2 1
0 0 1
4 -3 4
11 0 3
11 5 2

Output

YES

Input

4
2 2 2
7 2 3
7 7 2
2 7 3

Output

NO

Note

In the first sample, one can decrease the radii of the first and third disk by $0.5$, and increase the radius of the second disk by $0.5$. This way, the sum of all radii decreases by $0.5$. The situation before and after changing the radii is depicted below.

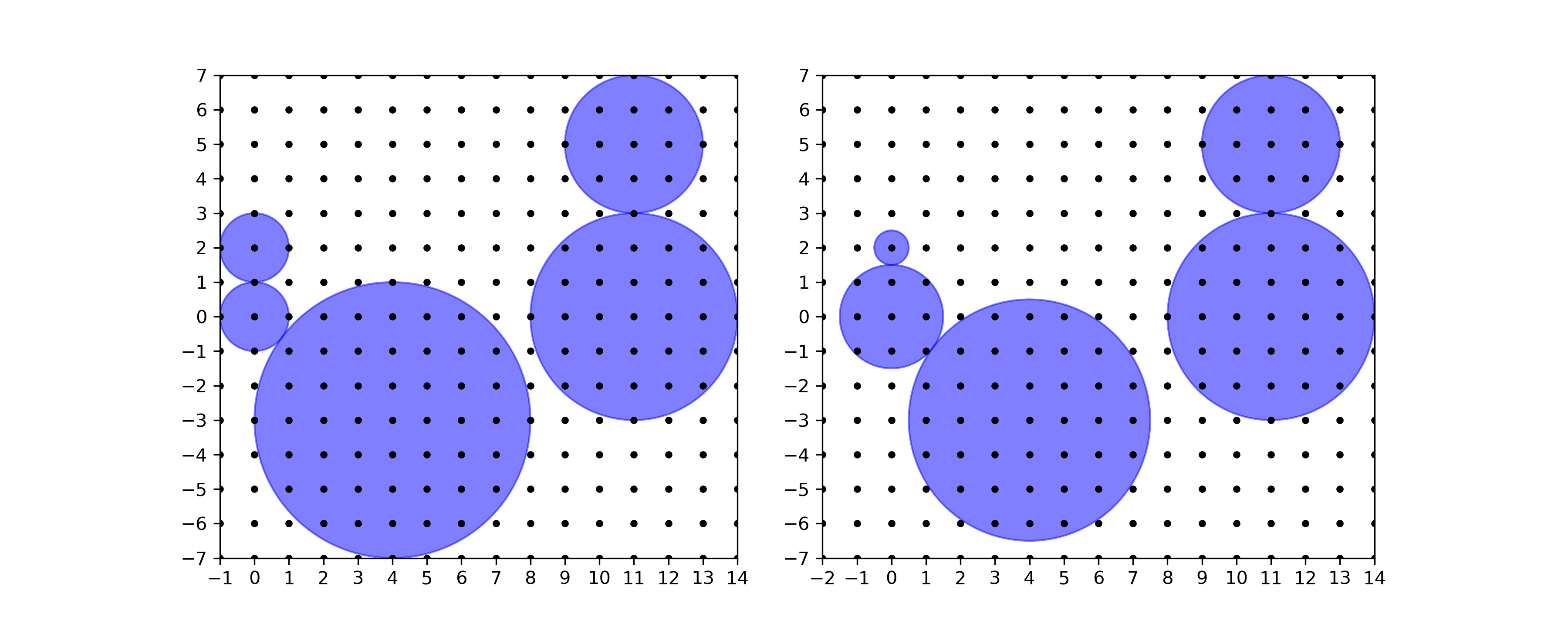First sample (left) and a valid way to change the radii of the disks (right).

In the second sample, depicted below, there is no way to change the radii of the disks in the desired manner.

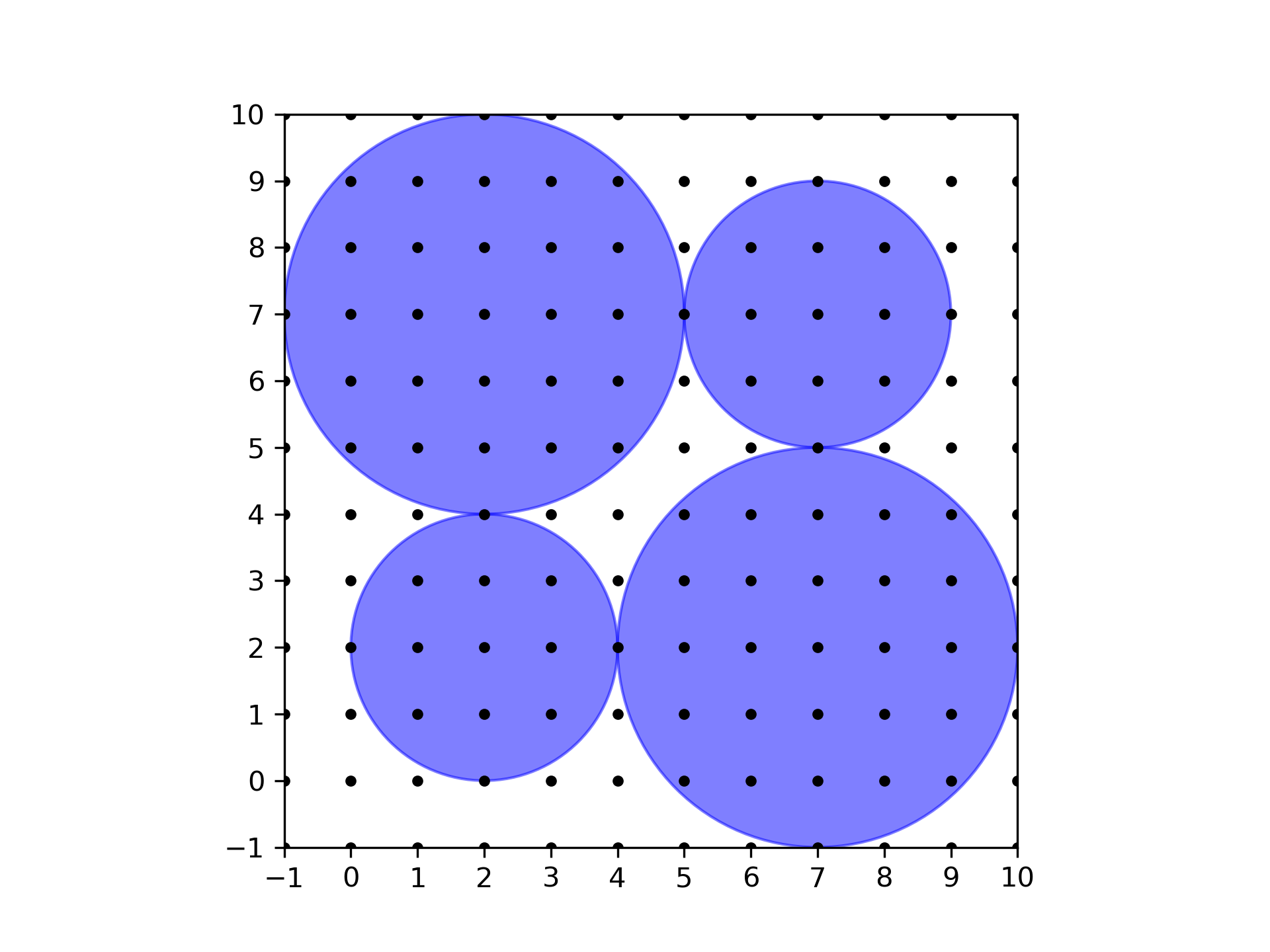Second sample.

题目大意：
你有一些平面上的圆盘，每个圆盘的中心有整数坐标，半径是正整数。任意两个圆盘不会在正面积区域重叠，但圆盘可以相切。你的任务是判断是否可以通过改变圆盘的半径，使得：

- 之前相切的圆盘仍然相切；
- 没有两个圆盘在正面积区域重叠；
- 所有圆盘半径之和严格减少。

新的半径可以是任意的正实数，圆盘的中心不能改变。

输入数据格式：
第一行包含一个整数 n (1≤n≤1000) — 圆盘的数量。
接下来 n 行，每行包含三个整数，分别代表一个圆盘的中心的 x 坐标、y 坐标 (-10^9 ≤ x, y ≤ 10^9) 和半径 r (1 ≤ r ≤ 10^9)。

输出数据格式：
如果可以按照要求改变半径，输出 "YES"。否则，输出 "NO"。

请注意，以上内容已经过翻译和简化处理，以适应中文读者的理解。题目大意： 你有一些平面上的圆盘，每个圆盘的中心有整数坐标，半径是正整数。任意两个圆盘不会在正面积区域重叠，但圆盘可以相切。你的任务是判断是否可以通过改变圆盘的半径，使得： - 之前相切的圆盘仍然相切； - 没有两个圆盘在正面积区域重叠； - 所有圆盘半径之和严格减少。 新的半径可以是任意的正实数，圆盘的中心不能改变。 输入数据格式： 第一行包含一个整数 n (1≤n≤1000) — 圆盘的数量。 接下来 n 行，每行包含三个整数，分别代表一个圆盘的中心的 x 坐标、y 坐标 (-10^9 ≤ x, y ≤ 10^9) 和半径 r (1 ≤ r ≤ 10^9)。 输出数据格式： 如果可以按照要求改变半径，输出 "YES"。否则，输出 "NO"。 请注意，以上内容已经过翻译和简化处理，以适应中文读者的理解。