311213: CF1950F. 0, 1, 2, Tree!

F. 0, 1, 2, Tree!time limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

Find the minimum height of a rooted tree$^{\dagger}$ with $a+b+c$ vertices that satisfies the following conditions:

• $a$ vertices have exactly $2$ children,
• $b$ vertices have exactly $1$ child, and
• $c$ vertices have exactly $0$ children.

If no such tree exists, you should report it.

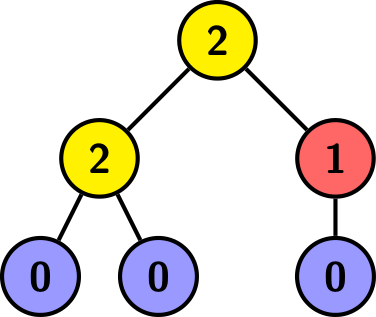
The tree above is rooted at the top vertex, and each vertex is labeled with the number of children it has. Here $a=2$, $b=1$, $c=3$, and the height is $2$.

$^{\dagger}$ A rooted tree is a connected graph without cycles, with a special vertex called the root. In a rooted tree, among any two vertices connected by an edge, one vertex is a parent (the one closer to the root), and the other one is a child.

The distance between two vertices in a tree is the number of edges in the shortest path between them. The height of a rooted tree is the maximum distance from a vertex to the root.

Input

The first line contains an integer $t$ ($1 \leq t \leq 10^4$) — the number of test cases.

The only line of each test case contains three integers $a$, $b$, and $c$ ($0 \leq a, b, c \leq 10^5$; $1 \leq a + b + c$).

The sum of $a + b + c$ over all test cases does not exceed $3 \cdot 10^5$.

Output

For each test case, if no such tree exists, output $-1$. Otherwise, output one integer — the minimum height of a tree satisfying the conditions in the statement.

ExampleInput

10
2 1 3
0 0 1
0 1 1
1 0 2
1 1 3
3 1 4
8 17 9
24 36 48
1 0 0
0 3 1

Output

2
0
1
1
-1
3
6
-1
-1
3

Note

The first test case is pictured in the statement. It can be proven that you can't get a height smaller than $2$.

In the second test case, you can form a tree with a single vertex and no edges. It has height $0$, which is clearly optimal.

In the third test case, you can form a tree with two vertices joined by a single edge. It has height $1$, which is clearly optimal.

题目大意：
给定三个整数a、b、c，分别代表有2个、1个、0个子节点的节点数量。要求找到一个树形结构，使得节点总数为a+b+c，并且满足上述子节点数量的条件。求这个树的最小高度。如果没有这样的树存在，则报告不存在。

输入数据格式：
第一行包含一个整数t，表示测试用例的数量。
接下来t行，每行包含三个整数a、b、c，分别代表有2个、1个、0个子节点的节点数量。

输出数据格式：
对于每个测试用例，如果不存在这样的树，则输出-1。否则，输出一个整数，表示满足条件的最小树高度。

公式用latex格式表示：
- 树的高度定义：$$
\text{height}(v) = \begin{cases}
0 & \text{if } v \text{ is a leaf} \\
1 + \max(\text{height}(w)) & \text{if } v \text{ has children } w_1, w_2, \ldots, w_k
\end{cases}
$$
- 最小树高度计算：$$
\text{minHeight}(a, b, c) = \begin{cases}
-1 & \text{if } a < b \text{ or } b < c \text{ or } a + b < c \\
\lceil \log_2(a + b + c) \rceil & \text{otherwise}
\end{cases}
$$题目大意： 给定三个整数a、b、c，分别代表有2个、1个、0个子节点的节点数量。要求找到一个树形结构，使得节点总数为a+b+c，并且满足上述子节点数量的条件。求这个树的最小高度。如果没有这样的树存在，则报告不存在。 输入数据格式： 第一行包含一个整数t，表示测试用例的数量。 接下来t行，每行包含三个整数a、b、c，分别代表有2个、1个、0个子节点的节点数量。 输出数据格式： 对于每个测试用例，如果不存在这样的树，则输出-1。否则，输出一个整数，表示满足条件的最小树高度。 公式用latex格式表示： - 树的高度定义：$$ \text{height}(v) = \begin{cases} 0 & \text{if } v \text{ is a leaf} \\ 1 + \max(\text{height}(w)) & \text{if } v \text{ has children } w_1, w_2, \ldots, w_k \end{cases} $$ - 最小树高度计算：$$ \text{minHeight}(a, b, c) = \begin{cases} -1 & \text{if } a < b \text{ or } b < c \text{ or } a + b < c \\ \lceil \log_2(a + b + c) \rceil & \text{otherwise} \end{cases} $$