311277: CF1959E. Jumping on Tiles

E. Jumping on Tilestime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Polycarp was given a row of tiles. Each tile contains one lowercase letter of the Latin alphabet. The entire sequence of tiles forms the string $s$.

In other words, you are given a string $s$ consisting of lowercase Latin letters.

Initially, Polycarp is on the first tile of the row and wants to get to the last tile by jumping on the tiles. Jumping from $i$-th tile to $j$-th tile has a cost equal to $|index(s_i) - index(s_j)|$, where $index(c)$ is the index of the letter $c$ in the alphabet (for example, $index($'a'$)=1$, $index($'b'$)=2$, ..., $index($'z'$)=26$) .

Polycarp wants to get to the $n$-th tile for the minimum total cost, but at the same time make maximum number of jumps.

In other words, among all possible ways to get to the last tile for the minimum total cost, he will choose the one with the maximum number of jumps.

Polycarp can visit each tile at most once.

Polycarp asks you to help — print the sequence of indices of string $s$ on which he should jump.

Input

The first line of the input contains an integer $t$ ($1 \le t \le 10^4$) — the number of test cases in the test.

Each test case is given by the string $s$ ($2 \le |s| \le 2 \cdot 10^5$), where $|s|$ — is the length of string $s$. The string $s$ consists of lowercase Latin letters.

It is guaranteed that the sum of string lengths $s$ over all test cases does not exceed $2 \cdot 10^5$.

Output

The answer to each test case consists of two lines.

In the first line print two integers $cost$, $m$, where $cost$ is the minimum total cost of the path, and $m$ is the maximum number of visited tiles Polycarp can make to get to $n$-th tiles for the minimum total cost $cost$ (i.e. the number of jumps is $m-1$).

In the next line print $m$ different numbers $j_1, j_2, \dots, j_m$ ($1 \le j_i \le |s|$) — the sequence of indices of the tiles Polycarp will jump on. The first number in the sequence must be $1$ (that is, $j_1=1$) and the last number must be the value of $|s|$ (that is, $j_m=|s|$).

If there are multiple answers, print any of them.

ExampleInput

6
logic
codeforces
bca
aaaaaaaaaaa
adbaadabad
to

Output

9 4
1 4 3 5
16 10
1 8 3 4 9 5 2 6 7 10
1 2
1 3
0 11
1 8 10 4 3 5 7 2 9 6 11
3 10
1 9 5 4 7 3 8 6 2 10
5 2
1 2

Note

In the first test case, the required path corresponds to the picture:

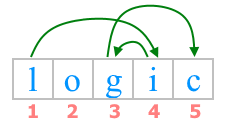
In this case, the minimum possible total cost of the path is achieved. Since $index($'l'$)=12$, $index($'o'$)=15$, $index($'g'$)=7$, $index($'i'$)=9$, $index($'c'$)=3$, then the total cost of the path is $|12-9|+|9-7|+|7-3|=3+2+4=9$.

题目大意：
Polycarp得到了一排瓦片，每个瓦片上有一个拉丁小写字母。这些瓦片构成了字符串s。

给定一个由拉丁小写字母组成的字符串s。

Polycarp最初站在这一排的第一块瓦片上，他想通过在瓦片上跳跃到达最后一块瓦片。从第i块瓦片跳到第j块瓦片的成本等于|index(s_i) - index(s_j)|，其中index(c)是字母c在字母表中的索引（例如，index('a')=1，index('b')=2，...，index('z')=26）。

Polycarp希望以最小的总成本到达第n块瓦片，但同时又想进行最大数量的跳跃。

换句话说，在所有可能以最小总成本到达最后一块瓦片的方式中，他会选择跳跃次数最多的一种。

Polycarp每个瓦片最多只能访问一次。

Polycarp请求你的帮助——打印他在跳跃时应该站在字符串s的索引序列。

输入数据格式：
第一行输入包含一个整数t（1≤t≤10^4）——测试用例的数量。

每个测试用例由字符串s（2≤|s|≤2*10^5）给出，其中|s|是字符串s的长度。字符串s由拉丁小写字母组成。

保证所有测试用例的字符串长度s的总和不超过2*10^5。

输出数据格式：
每个测试用例的答案由两行组成。

第一行打印两个整数cost，m，其中cost是路径的最小总成本，m是Polycarp为了以最小总成本到达第n块瓦片可以访问的最大瓦片数（即跳跃次数为m-1）。

在下一行打印m个不同的数字j_1, j_2, ..., j_m——Polycarp将跳跃的瓦片索引序列。序列中的第一个数字必须是1（即j_1=1），最后一个数字必须是s的长度（即j_m=|s|）。

如果存在多个答案，请打印其中任何一个。题目大意： Polycarp得到了一排瓦片，每个瓦片上有一个拉丁小写字母。这些瓦片构成了字符串s。 给定一个由拉丁小写字母组成的字符串s。 Polycarp最初站在这一排的第一块瓦片上，他想通过在瓦片上跳跃到达最后一块瓦片。从第i块瓦片跳到第j块瓦片的成本等于|index(s_i) - index(s_j)|，其中index(c)是字母c在字母表中的索引（例如，index('a')=1，index('b')=2，...，index('z')=26）。 Polycarp希望以最小的总成本到达第n块瓦片，但同时又想进行最大数量的跳跃。 换句话说，在所有可能以最小总成本到达最后一块瓦片的方式中，他会选择跳跃次数最多的一种。 Polycarp每个瓦片最多只能访问一次。 Polycarp请求你的帮助——打印他在跳跃时应该站在字符串s的索引序列。 输入数据格式： 第一行输入包含一个整数t（1≤t≤10^4）——测试用例的数量。 每个测试用例由字符串s（2≤|s|≤2*10^5）给出，其中|s|是字符串s的长度。字符串s由拉丁小写字母组成。 保证所有测试用例的字符串长度s的总和不超过2*10^5。 输出数据格式： 每个测试用例的答案由两行组成。 第一行打印两个整数cost，m，其中cost是路径的最小总成本，m是Polycarp为了以最小总成本到达第n块瓦片可以访问的最大瓦片数（即跳跃次数为m-1）。 在下一行打印m个不同的数字j_1, j_2, ..., j_m——Polycarp将跳跃的瓦片索引序列。序列中的第一个数字必须是1（即j_1=1），最后一个数字必须是s的长度（即j_m=|s|）。 如果存在多个答案，请打印其中任何一个。