311285: CF1965E. Connected Cubes

E. Connected Cubestime limit per test4 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

There are $n \cdot m$ unit cubes currently in positions $(1, 1, 1)$ through $(n, m, 1)$. Each of these cubes is one of $k$ colors. You want to add additional cubes at any integer coordinates such that the subset of cubes of each color is connected, where two cubes are considered connected if they share a face.

In other words, for every pair of cubes of the same color $c$, it should be possible to travel from one to the other, moving only through cubes of color $c$ that share a face.

The existing cubes are currently in the corner of a room. There are colorless cubes completely filling the planes $x = 0$, $y = 0$, and $z = 0$, preventing you from placing additional cubes there or at any negative coordinates.

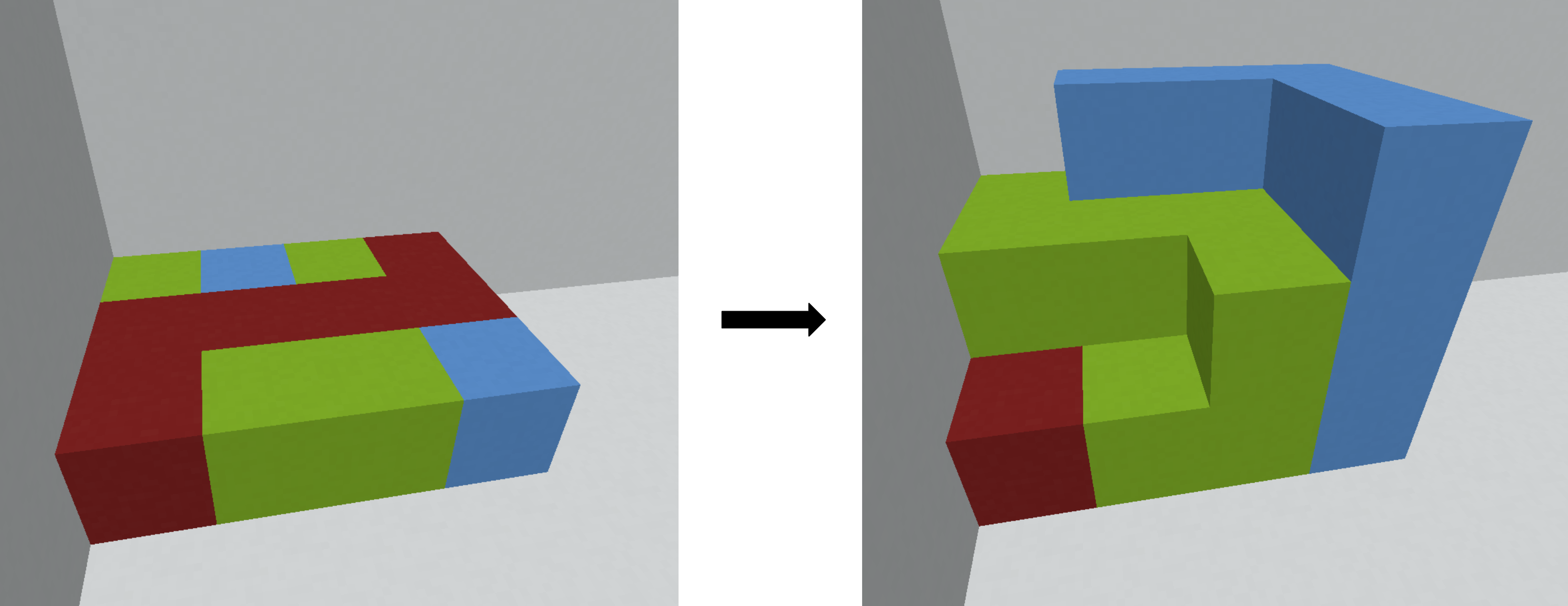
Find a solution that uses at most $4 \cdot 10^5$ additional cubes (not including the cubes that are currently present), or determine that there is no solution. It can be shown that under the given constraints, if there is a solution, there is one using at most $4 \cdot 10^5$ additional cubes.

Input

The first line of the input contains three integers $n$, $m$, and $k$ ($2 \le n, m, k \le 50$) — the number of rows and columns of cubes, and the number of colors, respectively.

The $i$-th of the next $n$ lines contains $m$ integers. The $j$-th of these is $a_{ij}$ ($1 \le a_{ij} \le k$) — the color of the cube at position $(i, j, 1)$. For every color from $1$ to $k$, it is guaranteed that there is at least one cube in the input of that color.

Output

If there is no solution, print a single integer $-1$.

Otherwise, the first line of output should contain a single integer $p$ ($0 \le p \le 4 \cdot 10^5$) — the number of additional cubes you will add.

The next $p$ lines should contain four integers $x$, $y$, $z$ and $c$ ($1 \le x, y, z \le 10^6$, $1 \le c \le k$) — indicating that you are adding a cube with color $c$ at position $(x, y, z)$.

No two cubes in the output should have the same coordinates, and no cube in the output should have the same coordinates as any cube in the input.

If there are multiple solutions, print any.

ExamplesInput

3 4 3
3 2 3 1
1 1 1 1
1 3 3 2

Output

13
1 1 2 3
1 3 2 3
2 1 2 3
2 2 2 3
2 3 2 3
3 3 2 3
1 2 2 2
1 2 3 2
1 3 3 2
1 4 3 2
2 4 3 2
3 4 3 2
3 4 2 2

Input

2 2 2
2 1
1 2

Output

9
1 3 1 1
2 3 1 1
3 1 1 1
3 2 1 1
3 3 1 1
1 1 2 2
1 2 2 2
2 1 2 2
2 2 2 2

Note

The image in the statement corresponds to the first example case, with $\text{red} = 1$, $\text{blue} = 2$, $\text{green} = 3$.

题目大意：
E. 连接的立方体

有n*m个单位立方体，位于坐标(1, 1, 1)到(n, m, 1)。这些立方体有k种颜色。你需要添加额外的立方体，使得每种颜色的立方体都是连通的，即两个立方体共享一个面。现有立方体位于房间的角落，有颜色无的立方体完全填满了平面x=0, y=0, z=0，阻止你放置额外的立方体。找到使用不超过4*10^5个额外立方体的解决方案，或者确定没有解决方案。

输入数据格式：
第一行包含三个整数n, m, k（2≤n, m, k≤50）——行数、列数和颜色数。
接下来n行，每行m个整数。第i行的第j个整数a_{ij}（1≤a_{ij}≤k）表示坐标(i, j, 1)处的立方体颜色。对于每种颜色从1到k，保证输入中至少有一个该颜色的立方体。

输出数据格式：
如果没有解决方案，输出一个整数-1。
否则，第一行输出一个整数p（0≤p≤4*10^5）——你将添加的额外立方体数量。
接下来p行，每行四个整数x, y, z和c（1≤x, y, z≤10^6，1≤c≤k）——表示你在坐标(x, y, z)添加一个颜色为c的立方体。
输出中的两个立方体不能有相同的坐标，输出的立方体不能与输入的立方体有相同的坐标。
如果有多个解决方案，输出任意一个。题目大意： E. 连接的立方体 有n*m个单位立方体，位于坐标(1, 1, 1)到(n, m, 1)。这些立方体有k种颜色。你需要添加额外的立方体，使得每种颜色的立方体都是连通的，即两个立方体共享一个面。现有立方体位于房间的角落，有颜色无的立方体完全填满了平面x=0, y=0, z=0，阻止你放置额外的立方体。找到使用不超过4*10^5个额外立方体的解决方案，或者确定没有解决方案。 输入数据格式： 第一行包含三个整数n, m, k（2≤n, m, k≤50）——行数、列数和颜色数。 接下来n行，每行m个整数。第i行的第j个整数a_{ij}（1≤a_{ij}≤k）表示坐标(i, j, 1)处的立方体颜色。对于每种颜色从1到k，保证输入中至少有一个该颜色的立方体。 输出数据格式： 如果没有解决方案，输出一个整数-1。 否则，第一行输出一个整数p（0≤p≤4*10^5）——你将添加的额外立方体数量。 接下来p行，每行四个整数x, y, z和c（1≤x, y, z≤10^6，1≤c≤k）——表示你在坐标(x, y, z)添加一个颜色为c的立方体。 输出中的两个立方体不能有相同的坐标，输出的立方体不能与输入的立方体有相同的坐标。 如果有多个解决方案，输出任意一个。