311368: CF1975E. Chain Queries
Description
You are given a tree of $n$ vertices numbered from $1$ to $n$. Initially, all vertices are colored white or black.
You are asked to perform $q$ queries:
- "u" — toggle the color of vertex $u$ (if it was white, change it to black and vice versa).
After each query, you should answer whether all the black vertices form a chain. That is, there exist two black vertices such that the simple path between them passes through all the black vertices and only the black vertices. Specifically, if there is only one black vertex, they form a chain. If there are no black vertices, they do not form a chain.
InputEach test contains multiple test cases. The first line contains the number of test cases $t$ ($1\leq t\leq 10^4$). The description of the test cases follows.
The first line of each test case contains two integers $n$ and $q$ ($1\leq n,q\leq 2\cdot 10^5$).
The second line of each test case contains $n$ integers $c_1,c_2,\ldots,c_n$ ($c_i \in \{ \mathtt{0}, \mathtt{1} \}$) — the initial color of the vertices. $c_i$ denotes the color of vertex $i$ where $\mathtt{0}$ denotes the color white, and $\mathtt{1}$ denotes the color black.
Then $n - 1$ lines follow, each line contains two integers $x_i$ and $y_i$ ($1 \le x_i,y_i \le n$), indicating an edge between vertices $x_i$ and $y_i$. It is guaranteed that these edges form a tree.
The following $q$ lines each contain an integer $u_i$ ($1 \le u_i \le n$), indicating the color of vertex $u_i$ needs to be toggled.
It is guaranteed that the sum of $n$ and $q$ over all test cases respectively does not exceed $2\cdot 10^5$.
OutputFor each query, output "Yes" if the black vertices form a chain, and output "No" otherwise.
You can output "Yes" and "No" in any case (for example, strings "yEs", "yes", "Yes" and "YES" will be recognized as a positive response).
ExamplesInput2 2 1 1 0 1 2 1 5 4 1 0 0 0 0 1 2 1 3 1 5 3 4 4 3 2 5Output
No No Yes Yes NoInput
4 5 3 1 1 1 1 1 3 5 2 5 3 4 1 5 1 1 1 4 4 0 0 0 0 1 2 2 3 1 4 1 2 3 2 1 1 1 1 1 1 0 1Output
Yes No Yes Yes Yes Yes No No YesNote
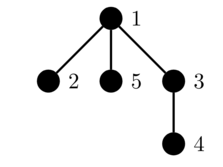
In the second test case, the color of the vertices are as follows:
The initial tree:
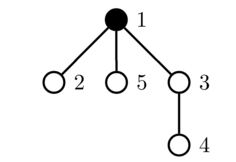
The first query toggles the color of vertex $4$:
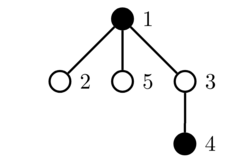
The second query toggles the color of vertex $3$:
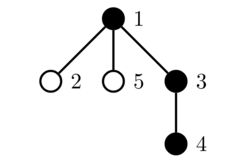
The third query toggles the color of vertex $2$:
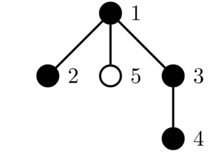
The fourth query toggles the color of vertex $5$:
Output
输入数据格式:每个测试包含多个测试用例。第一行包含测试用例的数量t(1≤t≤10^4)。接下来是每个测试用例的描述。
每个测试用例的第一行包含两个整数n和q(1≤n,q≤2×10^5)。
第二行包含n个整数c_1,c_2,…,c_n(c_i ∈ {0, 1})——顶点的初始颜色。c_i表示顶点i的颜色,其中0表示白色,1表示黑色。
然后是n-1行,每行包含两个整数x_i和y_i(1≤x_i,y_i≤n),表示顶点x_i和y_i之间的一条边。保证这些边构成一棵树。
接下来的q行,每行包含一个整数u_i(1≤u_i≤n),表示需要翻转顶点u_i的颜色。
保证所有测试用例的n和q之和不超过2×10^5。
输出数据格式:对于每个查询,如果黑色顶点形成一条链,输出"Yes",否则输出"No"。
输出可以是任何大小写形式的"Yes"和"No"。题目大意:给定一棵包含n个顶点的树,顶点编号从1到n。初始时,所有顶点被涂成白色或黑色。你需要执行q个查询,每次查询翻转一个顶点的颜色(如果它是白色,则变成黑色,反之亦然)。每次查询后,你需要回答所有黑色顶点是否形成一条链。链的定义是存在两个黑色顶点,使得它们之间的简单路径只经过黑色顶点。特别地,如果只有一个黑色顶点,它们形成一条链。如果没有黑色顶点,它们不形成链。 输入数据格式:每个测试包含多个测试用例。第一行包含测试用例的数量t(1≤t≤10^4)。接下来是每个测试用例的描述。 每个测试用例的第一行包含两个整数n和q(1≤n,q≤2×10^5)。 第二行包含n个整数c_1,c_2,…,c_n(c_i ∈ {0, 1})——顶点的初始颜色。c_i表示顶点i的颜色,其中0表示白色,1表示黑色。 然后是n-1行,每行包含两个整数x_i和y_i(1≤x_i,y_i≤n),表示顶点x_i和y_i之间的一条边。保证这些边构成一棵树。 接下来的q行,每行包含一个整数u_i(1≤u_i≤n),表示需要翻转顶点u_i的颜色。 保证所有测试用例的n和q之和不超过2×10^5。 输出数据格式:对于每个查询,如果黑色顶点形成一条链,输出"Yes",否则输出"No"。 输出可以是任何大小写形式的"Yes"和"No"。