311388: CF1979E. Manhattan Triangle

E. Manhattan Triangletime limit per test3 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard output

The Manhattan distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is defined as: $$|x_1 - x_2| + |y_1 - y_2|.$$

We call a Manhattan triangle three points on the plane, the Manhattan distances between each pair of which are equal.

You are given a set of pairwise distinct points and an even integer $d$. Your task is to find any Manhattan triangle, composed of three distinct points from the given set, where the Manhattan distance between any pair of vertices is equal to $d$.

Input

Each test consists of multiple test cases. The first line contains one integer $t$ ($1 \le t \le 10^4$) — the number of test cases. The description of the test cases follows.

The first line of each test case contains two integers $n$ and $d$ ($3 \le n \le 2 \cdot 10^5$, $2 \le d \le 4 \cdot 10^5$, $d$ is even) — the number of points and the required Manhattan distance between the vertices of the triangle.

The $(i + 1)$-th line of each test case contains two integers $x_i$ and $y_i$ ($-10^5 \le x_i, y_i \le 10^5$) — the coordinates of the $i$-th point. It is guaranteed that all points are pairwise distinct.

It is guaranteed that the sum of $n$ over all test cases does not exceed $2 \cdot 10^5$.

Output

For each test case, output three distinct integers $i$, $j$, and $k$ ($1 \le i,j,k \le n$) — the indices of the points forming the Manhattan triangle. If there is no solution, output "$0\ 0\ 0$" (without quotes).

If there are multiple solutions, output any of them.

ExampleInput

6
6 4
3 1
0 0
0 -2
5 -3
3 -5
2 -2
5 4
0 0
0 -2
5 -3
3 -5
2 -2
6 6
3 1
0 0
0 -2
5 -3
3 -5
2 -2
4 4
3 0
0 3
-3 0
0 -3
10 8
2 1
-5 -1
-4 -1
-5 -3
0 1
-2 5
-4 4
-4 2
0 0
-4 1
4 400000
100000 100000
-100000 100000
100000 -100000
-100000 -100000

Output

2 6 1
4 3 5
3 5 1
0 0 0
6 1 3
0 0 0

Note

In the first test case:

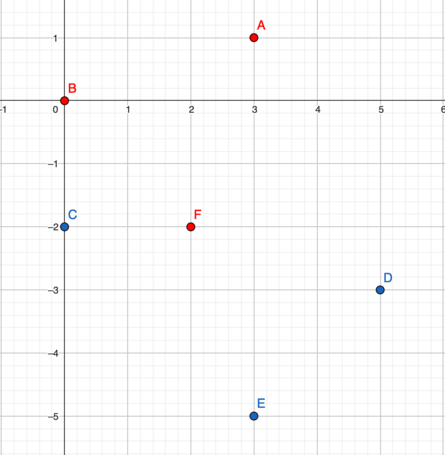Points $A$, $B$, and $F$ form a Manhattan triangle, the Manhattan distance between each pair of vertices is $4$. Points $D$, $E$, and $F$ can also be the answer.

In the third test case:

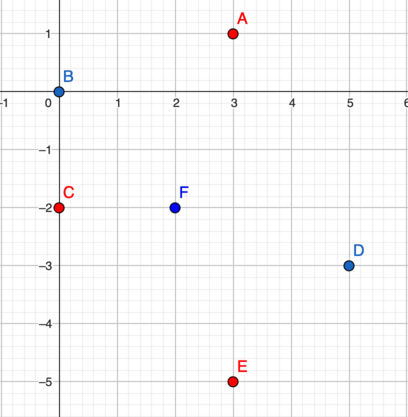Points $A$, $C$, and $E$ form a Manhattan triangle, the Manhattan distance between each pair of vertices is $6$.

In the fourth test case, there are no two points with a Manhattan distance of $4$, and therefore there is no suitable Manhattan triangle.

题目大意：在平面直角坐标系中，两点 $ (x_1, y_1) $ 和 $ (x_2, y_2) $ 之间的曼哈顿距离定义为 $ |x_1 - x_2| + |y_1 - y_2| $。如果三个点两两之间的曼哈顿距离相等，则称这三个点构成一个“曼哈顿三角形”。给定一组互不相同的点和一个偶数 $ d $，你的任务是找到任意一个由给定集合中的三个不同点构成的曼哈顿三角形，其中任意两个顶点之间的曼哈顿距离等于 $ d $。

输入数据格式：
- 第一行包含一个整数 $ t $，表示测试用例的数量。
- 每个测试用例的第一行包含两个整数 $ n $ 和 $ d $，分别表示点的数量和三角形顶点之间的曼哈顿距离。
- 接下来的 $ n $ 行，每行包含两个整数 $ x_i $ 和 $ y_i $，表示第 $ i $ 个点的坐标。
- 所有点的坐标保证互不相同。
- 所有测试用例中 $ n $ 的总和不超过 $ 2 \times 10^5 $。

输出数据格式：
- 对于每个测试用例，输出三个不同的整数 $ i $, $ j $, 和 $ k $，分别表示构成曼哈顿三角形的点的索引。
- 如果没有解决方案，输出 "0 0 0"（不带引号）。
- 如果有多个解决方案，输出其中任意一个。题目大意：在平面直角坐标系中，两点 $ (x_1, y_1) $ 和 $ (x_2, y_2) $ 之间的曼哈顿距离定义为 $ |x_1 - x_2| + |y_1 - y_2| $。如果三个点两两之间的曼哈顿距离相等，则称这三个点构成一个“曼哈顿三角形”。给定一组互不相同的点和一个偶数 $ d $，你的任务是找到任意一个由给定集合中的三个不同点构成的曼哈顿三角形，其中任意两个顶点之间的曼哈顿距离等于 $ d $。 输入数据格式： - 第一行包含一个整数 $ t $，表示测试用例的数量。 - 每个测试用例的第一行包含两个整数 $ n $ 和 $ d $，分别表示点的数量和三角形顶点之间的曼哈顿距离。 - 接下来的 $ n $ 行，每行包含两个整数 $ x_i $ 和 $ y_i $，表示第 $ i $ 个点的坐标。 - 所有点的坐标保证互不相同。 - 所有测试用例中 $ n $ 的总和不超过 $ 2 \times 10^5 $。 输出数据格式： - 对于每个测试用例，输出三个不同的整数 $ i $, $ j $, 和 $ k $，分别表示构成曼哈顿三角形的点的索引。 - 如果没有解决方案，输出 "0 0 0"（不带引号）。 - 如果有多个解决方案，输出其中任意一个。