400394: GYM100162 A Box Game

This problem is interactive — here you must implement an algorithm to play a game. Note that your program has to communicate via standard input and standard output (i.e., from the keyboard and to the screen). After writing each line, be sure to use the stream flushing function. Otherwise you risk leaving part of your output in I/O buffer. For example, you must use the fflush(stdout) function in С++, call System.out.flush() in Java, and flush(output) in Pascal.

Alice and Bob play the following box game. There are n boxes on the table in a row, numbered from 1 to n from left to right. For each box Alice and Bob know its capacity c_i — the maximal number of balls which can be placed in it. So the i-th box can contain any number of balls between 0 and c_i, inclusive. Initially the i-th box contains s_i balls.

Alice starts and the players take turns alternately. In a turn, a player should add a single ball into any box or take a single ball from any box. Obviously, a player can't place a ball into a box (say, i) if it already contains c_i balls. Similarly, a player can't take a ball from a box if the box is empty. There is one more rule: a player can make only such a move that leads to the situation that didn't happen before. In other words, a player can't make a move that leads to the game situation which already happened before. Obviously, it makes the game finite. A player loses if (s)he can't make a move.

You may assume that the balls are indistinguishable and the players have as many balls as may be needed in a game.

Write a program to play this game against the jury program. Your program should always win. You choose if you play for Alice or for Bob in each test case.

The input contains multiple test cases. The first line of each test case contains n (1 ≤ n ≤ 15) — the number of the boxes. The second line contains the sequence of integers c₁, c₂, ..., c_n (1 ≤ c_i ≤ 10 000) — the boxes' capacities. It is guaranteed that the number of all possible states in the game doesn't exceed 50 000, that is, 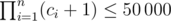. The third line contains the integers s₁, s₂, ..., s_n (0 ≤ s_i ≤ c_i) that give the initial arrangement of the balls.

A move description is a line containing an integer number p (1 ≤ p ≤ n) and a character '+' or '-', separated by a space. Character '+' means that a player places a ball into the p-th box, while character '-' means that a player removes a ball from the p-th box.

The rest of the test case contains lines with move descriptions of the opponent, one description per line. If you play for Alice, write your first move, read the first opponent's move, then write your second move and so on. If you play for Bob, the first move is made by the opponent. So you should read the first opponent's move, then write your first move, read the second move of the opponent and so on. When your opponent can not make a move, he writes '0 ?' instead of his move and the test case ends.

The input ends with n = 0. You should not process this test case.

For each test case, print "Alice" if you want to move first, and "Bob" otherwise. Then print move descriptions one per line. After writing each line, be sure to use the stream flushing function.

2
1 1
1 1
2 -
0 ?
1
4
2
1 +
0 ?
0

Alice
1 -
1 +
Bob
1 +