402361: GYM100738 G Constant speed
Description
George is driving his car on a road of length n. There are n + 1 signs on this road and they are indexed starting from 1 in the order they are seen. George likes to take notes, so he writes down all of the signs he has seen. His notes can be represented as a string s of length n + 1.
- If si is a digit, it marks the start of a speed limit restriction
- If si is ), it marks the end of a speed limit restriction
- If si is * , it means that it's a sign that can be ignored (we only care about speed restrictions)
An example of such a string is 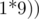 . Every start sign will have a corresponding end sign. In this case, those pairs are (1, 5) and (3, 4).
. Every start sign will have a corresponding end sign. In this case, those pairs are (1, 5) and (3, 4).
Between signs i and i + 1, the restriction that is applied is the one corresponding to the last previously seen start sign (its index is ≤ i) without an end pair (check samples for clarification).
George asks himself: What is the minimum number of pairs of signs that need to be removed such that the speed limit between signs a and b is constant? He needs to answer q such questions, so he needs your help.
InputThe first line will contain two integers, n and q(1 ≤ n, q ≤ 100 000) – the length of the road and the number of questions. The second line will contain a string s of length n + 1.
OutputYou should print q lines. On line i you should print the answer to the ith question.
ExamplesInput4 4Output
1*9))
2 4
2 3
1 5
4 5
1Input
0
1
0
5 1Output
55)5))
1 6
0Note
The speed limits in the first sample are:
- Between signs 1 and 2 the speed limit is 1
- Between signs 2 and 3 the speed limit is 1
- Between signs 3 and 4 the speed limit is 9
- Between signs 4 and 5 the speed limit is 1
In order to make the speed limit constant between the signs 2 and 4, we must delete the pair of signs (3, 4).