402816: GYM100886 K Toll Roads

There are n cities in the country of Flatland, n - 1 bidirectional roads connect some pairs of Flatland's cities. It is possible to get from any city to any other city of the country using roads. In this problem we will refer to the smallest set of roads needed to travel from a to b as a simple path.

The government of Flatland has recently introduced payment tolls on all roads. Using one road connecting two cities costs one ruble. That means that every time when you travel from one city to another one, you have to pay as many rubles as the number of roads you pass during your journey.

Many people got upset because of this decision, especially people who travel long distances. Political opponents of the current government claim that the maximal cost of a simple path in Flatland is very high, namely 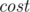rubles. The government has decided to support people and calm down the opposition. They want to reduce the maximal cost of a simple path in the country as much as possible. In other words, they want the number 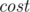reported by the opposition to be the lowest possible. The government will allow to remove tolls from at most k roads in order to achieve that. If there are multiple ways to do that, they want to minimize the number of roads that will become free.

Like any other government, Flatland's one is quite inflexible. They additionally require that it should be possible to represent the set of roads which will become free as a simple path between some cities x and y. Your task is to help the government.

The first line contains two integers n and k (1 ≤ k < n ≤ 5000), the number of cities in Flatland and the maximum number of roads to become toll-free, respectively. Each of the next n - 1 lines contains two integers u_i and v_i, meaning that there is a road connecting cities u_i and v_i (0 ≤ u_i, v_i < n).

On the first line of the output, print one integer: the minimum 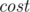of the most expensive simple path in Flatland that the government can achieve (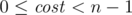). On the second line, print the minimum number of roads t that must be made free to achieve that 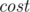(0 ≤ t ≤ k). If t > 0, print two space-separated integers on the third line: the numbers of cities x and y such that all roads on the simple path between them must be made free (0 ≤ x, y < n, the simple path between x and y must contain exactly t roads).

8 3
0 2
0 5
2 3
5 1
4 5
5 6
6 7

2
3
2 6

5 2
0 1
0 2
0 3
0 4

2
0