403291: GYM101102 K Topological Sort

Consider a directed graph G of N nodes and all edges (u→v) such that u < v. It is clear that this graph doesn’t contain any cycles.

Your task is to find the lexicographically largest topological sort of the graph after removing a given list of edges.

A topological sort of a directed graph is a sequence that contains all nodes from 1 to N in some order such that each node appears in the sequence before all nodes reachable from it.

The first line of input contains a single integer T, the number of test cases.

The first line of each test case contains two integers N and M (1 ≤ N ≤ 10⁵) 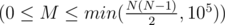, the number of nodes and the number of edges to be removed, respectively.

Each of the next M lines contains two integers a and b (1 ≤ a < b ≤ N), and represents an edge that should be removed from the graph.

No edge will appear in the list more than once.

For each test case, print N space-separated integers that represent the lexicographically largest topological sort of the graph after removing the given list of edges.

3
3 2
1 3
2 3
4 0
4 2
1 2
1 3

3 1 2
1 2 3 4
2 3 1 4