403548: GYM101192 J Covering distance

You are given a set of n geometric points. Assume arbitrary point P and all possible k non-degenerate different triangles T_i formed by point P and two other points within the set. Two triangles are considered different if they differ by at least one vertex. There are m_i points t_i, j situated strictly within T_i (points on the borders are excluded). Let's determine cover distance as 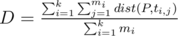, where dist(X, Y) means Euclidean distance between points X and Y. When there are no applicable points t_i, j for point P, then cover distance is equal to -1.

You are required to compute cover distance for each point of the set.

The first line contains number of points n. Following that are n lines, where the i^th line contains coordinates of the i^th point represented by two integer numbers x_i y_i. It is guaranteed that all points are distinct.

For each point p output the required average distance. If no point satisfies the above requirements, output  - 1. Your output should have an absolute or relative error of at most 10^- 9.

6
0 2
2 4
-1 3
0 0
1 3
1 2

-1
1.885618083
1.648528137
2.290569415
1.414213562
1