403668: GYM101237 E Another Short Problem

Consider an initial set A consisting of N points in three-dimensional space. Each point is associated with a real value p_i that is equal to the probability that i-th point is included in the final set B. Your task is to calculate the expected number of border points for convex hull of B.

A point is called a border point for the convex hull of set B if there is no way to choose points 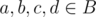such that p lies strictly inside the tetrahedron abcd.

The first line contains the number of points N (1 ≤ N ≤ 50). The next N lines describe points of A in the form p_i x_i y_i z_i, which are the probability of the i-th point to be included in the final set and the coordinates of the i-th point (0.00 ≤ p_i ≤ 1.00,  - 1000 ≤ x_i, y_i, z_i ≤ 1000). Probabilities are given with exactly two digits after the decimal point.

It is guaranteed that no two points of A coincide, no three points of A are collinear and no four points of A are coplanar.

Output the expected number of border points. Your answer will be considered correct if its absolute error is less then 10^- 6.

5
0.20 0 0 0
0.40 0 0 4
0.60 0 4 0
0.80 4 0 0
0.50 1 1 1

2.4808000000