404246: GYM101466 K Random Numbers

Tamref love random numbers, but he hates recurrent relations, Tamref thinks that mainstream random generators like the linear congruent generator suck. That's why he decided to invent his own random generator.

As any reasonable competitive programmer, he loves trees. His generator starts with a tree with numbers on each node. To compute a new random number, he picks a rooted subtree and multiply the values of each node on the subtree. He also needs to compute the number of divisors of the generated number (because of cryptographical applications).

In order to modify the tree (and hence create different numbers on the future), Tamref decided to perform another query: pick a node, and multiply its value by a given number.

Given a initial tree T, where T_u corresponds to the value on the node u, the operations can be summarized as follows:

• RAND: Given a node u compute 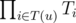and count its divisors, where T(u) is the set of nodes that belong to the subtree rooted at u.
• SEED: Given a node u and a number x, multiply T_u by x.

Tamref is quite busy trying to prove that his method indeed gives integers uniformly distributed, in the meantime, he wants to test his method with a set of queries, and check which numbers are generated. He wants you to write a program that given the tree, and some queries, prints the generated numbers and count its divisors.

Tamref has told you that the largest prime factor of both T_u and x is at most the Tamref's favourite prime: 13. He also told you that the root of T is always node 0.

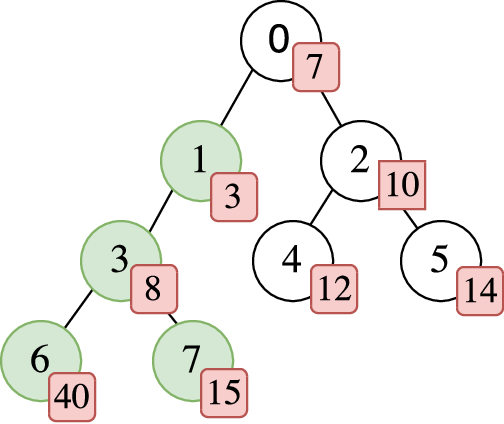
The figure shows the sample test case. The numbers inside the squares are the values on each node of the tree. The subtree rooted at node 1 is colored. The RAND query for the subtree rooted at node 1 would generate 14400, which has 63 divisors.

The first line is an integer n (1 ≤ n ≤ 10⁵), the number of nodes in the tree T. Then there are n - 1 lines, each line contains two integers u and v (0 ≤ u, v < n) separated by a single space, it represents that u is a parent of v in T. The next line contains n integers, where the i - th integer corresponds to T_i (1 ≤ T_i ≤ 10⁹). The next line contains a number Q (1 ≤ Q ≤ 10⁵), the number of queries. The final Q lines contain a query per line, in the form "RAND u" or "SEED u x" (0 ≤ u < n, 1 ≤ x ≤ 10⁹).

For each RAND query, print one line with the generated number and its number of divisors separated by a space. As this number can be very long, the generated number and its divisors must be printed modulo 10⁹ + 7.

8
0 1
0 2
1 3
2 4
2 5
3 6
3 7
7 3 10 8 12 14 40 15
3
RAND 1
SEED 1 13
RAND 1

14400 63
187200 126