404417: GYM101502 I Move Between Numbers

You are given n magical numbers a₁, a₂, ..., a_n, such that the length of each of these numbers is 20 digits.

You can move from the i^th number to the j^th number, if the number of common digits between a_i and a_j is exactly 17 digits.

The number of common digits between two numbers x and y is computed is follow:

.

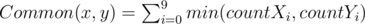Where countX_i is the frequency of the i^th digit in the number x, and countY_i is the frequency of the i^th digit in the number y.

You are given two integers s and e, your task is to find the minimum numbers of moves you need to do, in order to finish at number a_e starting from number a_s.

The first line contains an integer T (1 ≤ T ≤ 250), where T is the number of test cases.

The first line of each test case contains three integers n, s, and e (1 ≤ n ≤ 250) (1 ≤ s, e ≤ n), where n is the number of magical numbers, s is the index of the number to start from it, and e is the index of the number to finish at it.

Then n lines follow, giving the magical numbers. All numbers consisting of digits, and with length of 20 digits. Leading zeros are allowed.

For each test case, print a single line containing the minimum numbers of moves you need to do, in order to finish at number a_e starting from number a_s. If there is no answer, print -1.

1
5 1 5
11111191111191111911
11181111111111818111
11811171817171181111
11111116161111611181
11751717818314111118

3

In the first test case, you can move from a₁ to a₂, from a₂ to a₃, and from a₃ to a₅. So, the minimum number of moves is 3 moves.