404505: GYM101521 I RNG

RNG stands for Random Number Generator. Most RNGs are, in fact, psuedorandom number generators, which generate numbers that look random but are actually not. One of the simplest RNGs, which is called a linear congruential generator, works as follows:

1. The values of a, b, m, and X₁ are determined.
2. The sequence {X_n} is generated using the rule .

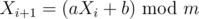In this problem, we consider a slightly more complicated RNG, which works as follows:

1. The values of a, b, c, d, m, and X₁ are determined.
2. The sequence {X_n} is generated using the rule .

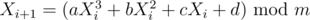A sequence of 15 integers was generated using the aforementioned RNG. The sequence consisted solely of integers 1, 2, 3, and 4. Unfortunately, some data — including the parameters a, b, c, d, m, and X₁, as well as some of the values of the integer sequence — is lost.

Your task is to recover any possible values of the parameters a, b, c, d, m, and X₁, given the remaining values of the integer sequence. You do not need to recover the sequence, since it only depends on the parameters.

Your parameters must satisfy the following constraints:

• 0 ≤ a, b, c, d ≤ 1023
• 1 ≤ m ≤ 65535
• Let the generated sequence be {Y_n}. Then 1 ≤ Y_i ≤ 4
• If the value of X_i is not lost, then Y_i = X_i

The first and only line of input consists of a string with exactly 15 characters. The i-th character is ? if the value of X_i is lost. Otherwise, the i-th character is one of 1, 2, 3, 4, representing the value of X_i.

It is guaranteed that the first character, representing the value of X₁, is a ?.

If there exist valid values for the parameters a, b, c, d, m, and X₁, output their values in that order separated by spaces.

If there is more than one solution, you may output any one.

If there is no solution, output -1 -1 -1 -1 -1 -1.

????12341234123

6 4 7 5 20 1

?222?222?222???

0 0 1 0 3 2

?23411111111111

-1 -1 -1 -1 -1 -1