404513: GYM101522 E Expected Score

As the army of Byteland is getting stronger and stronger, Hackson, the King of Hackerland, decides to establish a better relationship with Byteland. The King of Byteland, who loves playing games, asked Hackson to play a game with him.

The rule of the game is as follows:

On the border between Byteland and Hackerland, there are 2 × N chests. The inner surface of each chest is marked with a number which ranges from 1 to N. The King of Byteland told Hackson that every number appears exactly two times, but since all the chests are closed, Hackson has no idea what numbers are marked on the inside of the chests.

Each round, Hackson can choose two different chests and open them at the same time. If the numbers marked on both chosen chests are the same, the score of this round will be equal to that number. Otherwise, the score of this round will be zero. Both chests, whether the marked numbers are the same or not, are then closed and remain in the game.

The game will last for R rounds, and the final score of the game will be the highest score among all rounds.

Currently, R - 1 rounds have passed. Hackson would like to know, if he chooses two chests in the final round that maximizes his expected final score, what will his expected final score be?

The first line consists of two integers N and R. (1 ≤ N, R ≤ 10⁵)

The next R - 1 lines each consists of four integers x, y, C_x and C_y, which means that in the i-th round, the x-th and the y-th chest are chosen, and they are found out to be marked with numbers C_x and C_y respectively. (1 ≤ x, y ≤ 2N, x ≠ y, 1 ≤ C_x, C_y ≤ N)

It is guaranteed that the given information is valid and consistent.

Output a number, the expected final score of Hackson if he plays wisely in the final round.

Your answer will be accepted if the relative error or absolute error, whichever is less, is not greater than 10^- 6.

3 3
1 3 1 3
2 4 2 3

3

2 1

0.5

3 2
1 4 2 2

2.166667

In the first sample, there are a total of 6 chests. The score for the first 2 rounds are 0 but since Hackson has already opened the two chests marked with number 3, the optimal strategy is to choose those two chests in the final round. Therefore the maximum expected final score is 3.

In the second sample, there are a total of 4 chests, so Hackson has no information about the chests, which means Hackson can only choose two chests at random. He has chance of opening two chests marked with 1 and scoring 1 point, chance of opening two chests marked with 2 and scoring 2 points, of choosing two chests marked with different numbers and scoring zero. Therefore, his expected final score is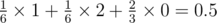

In the third sample, there are a total of 6 chests. In round 1, Hackson scored 2 points. In the last round, Hackson's optimal strategy is to choose any two unknown chests. There is chance that the two chests are marked with 3, which makes the final score 3. Therefore the maximum expected score is