405157: GYM101807 I Infection

Byteland is a country consisting of $$$N$$$ cities, numbered from $$$1$$$ to $$$N$$$, and they are connected by $$$M$$$ bidirectional roads. It is possible to reach each city from any other. Each road connects two cities $$$a$$$ and $$$b$$$. Two cities are neighbor if and only if they are directly connected by a road.

Scientists in Byteland found out that there will be an outbreak of Virus B in the coming weeks. The virus will first appear in one of the $$$N$$$ cities, make it into an infected city. Then, on each day the virus will spread to exactly one uninfected city which is neighbor to an infected city. the The infection process will end when all $$$N$$$ cities become infected.

As Virus B is a fatal and strong virus, they want to make some precautions against Virus B to minimize the impacts. Luckily, the scientists found out that Virus B has similar DNA structure with another Virus A, which appeared in Byteland 100 years ago, so the scientists predict that Virus B will infect different cities in a similar way as Virus A. More precisely, let the order of cities infected by Virus A be $$$A_1, A_2,\dots ,A_N$$$ and the order of cities infected by Virus B be $$$B_1, B_2, \dots, B_N$$$, the scientists predict that $$$B$$$ will be the lexicographically smallest ordering such that is also lexicographically greater than $$$A$$$.

An ordering $$$P_1, P_2, \dots, P_N$$$ is considered lexicographically smaller than another ordering $$$Q_1, Q_2, \dots, Q_N$$$, if $$$P_i < Q_i$$$, for the first $$$i$$$ where $$$P_i$$$ and $$$Q_i$$$ differ.

Given the structure of Byteland and the infection log of Virus A, please help the scientists to predict the order of cities infected by Virus B or print $$$-1$$$ if such ordering does not exist.

The first line contains two integers $$$N$$$ and $$$M$$$, the number of cities and roads in Byteland $$$(1 \le N, M \le 10^5)$$$.

The following $$$M$$$ line contains two integers $$$u_i$$$ and $$$v_i$$$, describing the $$$i^{th}$$$ road connecting city $$$u_i$$$ and $$$v_i$$$ $$$(1 \le u_i, v_i \le N)$$$.

The last line contains $$$N$$$ integers $$$A_i$$$, describing the order of cities infected by Virus A 100 years ago.

It is guaranteed that it is possible to reach each city from any other in Byteland. Also, it is guaranteed that the given ordering must be a valid infection ordering.

Output $$$N$$$ integers in the first line, the predicted infection ordering of Virus B. If such ordering does not exist, output $$$-1$$$ in the first line.

4 4
1 2
1 3
1 4
3 4
3 1 2 4

3 1 4 2

4 3
1 2
2 3
3 4
4 3 2 1

-1

In the first sample, the order of cities infected by Virus A is as follow:

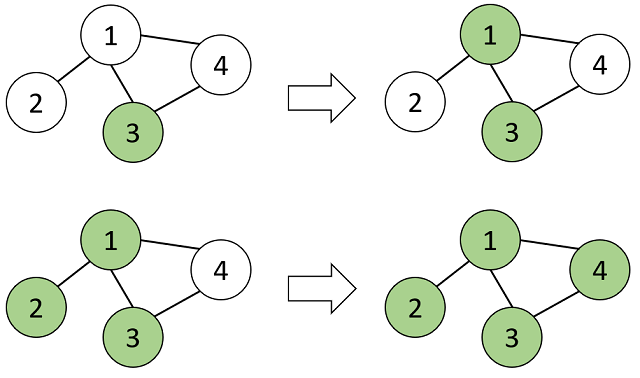
Therefore, the lexicographically smallest infection order for Virus B, which is lexicographically greater than infection order for Virus A, is $$$3, 1, 4, 2$$$