405158: GYM101807 J Jakanda Forever
Description
In East Hackerland, there is a country called Jakanda which possesses highly advanced technology. It consists of $$$N$$$ cities and $$$N - 1$$$ bidirectional roads. Each road has its own length and connects two cities. It is possible to travel from a city to any other city via these roads.
The Black Panda, king of Jakanda, is facing a problem. Some of the cities are having riot. A city under riot would send out a rebel army and try to capture one other city ("targeted city"). Black Panda is not going to let it happen. He would send a scout from the targeted city to the city under riot. Both the rebel and scout will walk for 1 mile toward their own destination during the day and rest at night. The scout would only spot the rebel army only if they are at the same location and it is at night. If the scout fails to spot the army, the rebel army would capture its target city.
Other than the riot, the length of some of the roads in Jakanda would change due to damage of the war.
Now there are $$$Q$$$ events in chronological order. Each event is one of the two types:
1 $$$u$$$ $$$v$$$, which denote city $$$u$$$ is now under riot and is sending a rebel army to capture city $$$v$$$. Note that city $$$v$$$ might have rebellion or captured before, but in these cases we would consider Black Panda had already suppressed it.
2 $$$i$$$ $$$l$$$, which denote the $$$i^{th}$$$ road is now changed to length $$$l$$$.
For each type 1 event, output JAKANDA FOREVER if the scout could spot the rebels, output WE NEED BLACK PANDA otherwise.
InputThe first line contains a single integer $$$N$$$, the number of cities ($$$1\le N\le 5\times 10^5$$$).
The following $$$N - 1$$$ lines contains the roads information, each line contains three integers: $$$u_i$$$, $$$v_i$$$ and $$$l_i$$$, which means the $$$i^{th}$$$ road connect city $$$u_i$$$ and $$$v_i$$$ with length of $$$l_i$$$ miles ($$$1\le u_i, v_i\le N$$$; $$$u_i\neq v_i$$$; $$$1\le l_i\le 10^9$$$).
Then a single line is followed, which contains a single integer $$$Q$$$ ($$$1 \le Q\le 5\times 10^5$$$).
The following $$$Q$$$ lines contains the event information, each line contains three integer. The first integer $$$type$$$ denote the event type.
For $$$type = 1$$$, two integers, $$$u$$$ $$$v$$$ is followed. $$$u$$$ is the city under riot and $$$v$$$ is the target city ($$$1\le u, v\le N$$$; $$$u\neq v$$$).
For $$$type = 2$$$, two integers, $$$i$$$ $$$l$$$ is followed. It means the $$$i^{th}$$$ road's length is changed to $$$l$$$ miles.
OutputFor each type 1 event, output JAKANDA FOREVER if the scout is going to spot the rebels, WE NEED BLACK PANDA otherwise.
ExampleInput4Output
1 2 3
1 3 4
4 1 5
5
1 1 2
1 2 3
2 1 2
1 2 1
1 4 2
WE NEED BLACK PANDANote
WE NEED BLACK PANDA
JAKANDA FOREVER
WE NEED BLACK PANDA
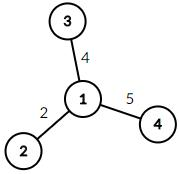
The structure of Jakanda before the third event: 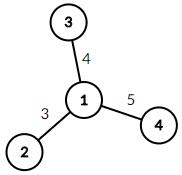
The structure of Jakanda after the third event: