405208: GYM101845 E Equilateral Triangles
Description
Yeison drew an equilateral triangle of side length n cm. Then for each side of the triangle he drew n - 1 lines parallel to it, with 1 cm of separation between them. Now the big triangle contains n2 equilateral small triangles of side length 1.
Let S be the set of all points that are vertices of any of the small triangles, now he is interested in knowing how many different pairs of points {a, b} where 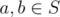 contain some other point
contain some other point 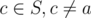 and c ≠ b in the line segment ab, two pairs {a1, b1} and {a2, b2} are considered equal if a1 = a2 and b1 = b2 or if a1 = b2 and b1 = a2, two pairs are different if they are not equal.
and c ≠ b in the line segment ab, two pairs {a1, b1} and {a2, b2} are considered equal if a1 = a2 and b1 = b2 or if a1 = b2 and b1 = a2, two pairs are different if they are not equal.
For n = 3 the triangle drew by him would be the following:
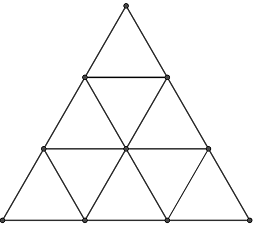
Help Yeison to solve this problem.
InputThe input consist of a single integer n (1 ≤ n ≤ 50) - the length of the triangle drew by Yeison.
OutputPrint one single integer - the answer of the problem.
ExamplesInput2Output
3Input
3Output
12