405251: GYM101858 C Chimera Ant King
Description
Meruem, the King of Chimera Ants, decided to be the best player of every game in the world.
Of course some games are played by a single player, so it's not easy to decide which player is the best at it. The criteria Meruem decided to use was how much time the player could finish the game, be lower the better.
You are to compete against Meruem on a very unique game: Sudoku Killer. He thinks you are the best player in the world, but just in case he is mistaken you are going to play the child's version.
Child Sudoku Killer is played on a $$$6 \times 6$$$ grid, divided in six $$$2 \times 3$$$ disjoint blocks. Also, the grid is divided into disjoint regions, each being a connected and have a value. Every grid cell is contained by exactly one block and one region.
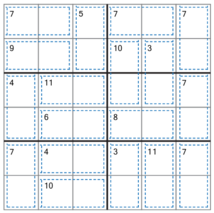
To finish the game, the following rules must meet:
- Each grid cell must have exactly one value between $$$1$$$ and $$$6$$$, inclusive.
- Each lines, column, block and region's cells must have different values.
- The sum of region cell's values must be equal to the region value.
You must finish the game as fast as possible. Show Meruem the solution.
InputThe first line contains one integer, $$$n$$$ ($$$6 \le n \le 36$$$) — the number of regions.
The second line contains $$$n$$$ integers, $$$v_i$$$ ($$$1 \le v_i \le 21$$$) — the value of the $$$i$$$-th region.
The next $$$6$$$ lines contains, each, $$$6$$$ integers, $$$r_{ij}$$$ ($$$1 \le r_{ij} \le n$$$) — the region of the cell in $$$i$$$-th line and $$$j$$$-th column.
It's guaranteed that the given board satisfies all game rules and that it has at least one solution.
OutputPrint $$$6$$$ lines, each having $$$6$$$ space-separated integers between $$$1$$$ and $$$6$$$, inclusive — the solution of the game.
If there are multiple solutions, print any of them.
ExamplesInput18Output
7 5 7 7 9 10 3 4 11 7 6 8 7 4 3 11 7 10
01 01 02 03 03 04
05 05 02 06 07 04
08 09 09 06 07 10
08 11 11 12 12 10
13 14 14 15 16 17
13 18 18 15 16 17
6 1 2 3 4 5Input
4 5 3 6 1 2
3 6 5 4 2 1
1 2 4 5 3 6
5 3 1 2 6 4
2 4 6 1 5 3
6Output
21 21 21 21 21 21
01 01 01 01 01 01
02 02 02 02 02 02
03 03 03 03 03 03
04 04 04 04 04 04
05 05 05 05 05 05
06 06 06 06 06 06
1 2 3 4 5 6
4 5 6 1 2 3
2 1 4 3 6 5
3 6 5 2 1 4
5 3 1 6 4 2
6 4 2 5 3 1