405304: GYM101879 A Studying level curves
Description
The Institute of Geography and Territorial Organization of the University of Lisbon (IGOT, in Portuguese), is conducting research projects at Pico Island. One of the research projects concerns the level curves of Mount Pico, the highest mountain in Portugal. Using image processing software, the researchers transform such curves into simple polygons (that do not self intersect).
To understand how the terrain changes with respect to height, IGOT is interested in the monotonicity of a level curve with respect to a set of directions (vectors). Given a vector $$$v$$$, we say that a simple polygon is $$$v$$$-monotone if any non-empty intersection of a straight line orthogonal to $$$v$$$ with the polygon is a segment (or a single point). You are one of the IGOT developers and they entrusted you with the following task. Given a simple polygon and a set of vectors, determine for each vector if the polygon is monotone with respect to this vector.
InputThe first line has two integers $$$N$$$ and $$$Q$$$, the number of vertices of the polygon and the number of queries, respectively. Each of the next $$$N+Q$$$ lines has two integers. The $$$i$$$th of these lines represents the point $$$(x_i,y_i)$$$ if $$$i \leq N$$$; otherwise it represents the vector $$$(v_x, v_y)$$$. The polygon vertices are listed in counter clockwise order.
Constraints
- $$$1 \leq N, Q \leq 10^5$$$
- $$$-10^9 \leq x_i, y_i, v_x, v_y \leq 10^9$$$
- You may assume that the polygon has positive area.
For each query, print "Y" (without quotes) if the polygon is monotone with respect to the corresponding vector, otherwise print "N".
ExamplesInput6 2Output
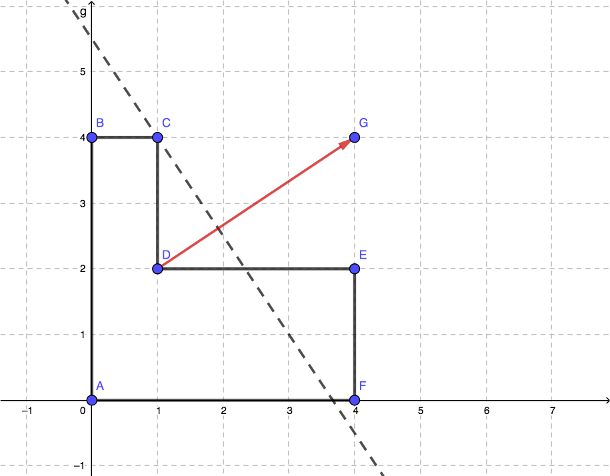
4 0
4 2
1 2
1 4
0 4
0 0
0 1
3 2
YInput
N
6 4Output
0 0
16 2
0 10
-10 0
0 -10
20 -4
10 10
10 -10
0 -20
-20 10
NNote
N
Y
N
In Figure $$$1$$$ we display the polygon of the first example and the vector $$$\overrightarrow{DG}$$$ that represents the second query.