405340: GYM101908 J Joining Capitals

A far far away kingdom has $$$N$$$ cities, among which $$$K$$$ are capitals. King Richard wants to build transmission lines, each one directly connecting two cities. Also, there needs to be a path, i.e. a sequence of transmission lines, between any pair of capitals.

Each transmission line has an associated cost, which is the Euclidean distance between the two cities that the transmission line connects. As the king is greedy, he wishes that the transmission lines are set up so that the total cost (sum of the costs for each line) is kept as small as possible.

The figure A shows an example of a kingdom with $$$N = 10$$$ cities and $$$K = 4$$$ capitals. The Chief Engineer reported to the king the solution shown in figure B. Such solution, in fact, minimizes the total cost. But the king didn't like to see a capital with more than one transmission line. He then determined a new restriction: a capital can be connected to only one other city. That way, after working a lot, Chief Engineer presented the new solution, illustrated in figure C. He's just not so sure if this is the optimal solution, so he needs your help.

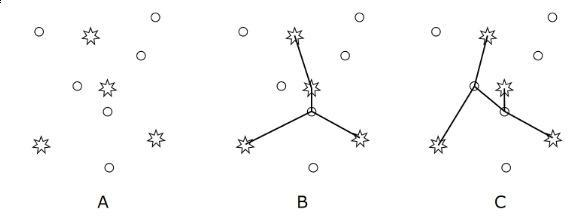
Given the coordinates of the cities, your program should compute the smallest total cost to build transmission lines so that every pair of capitals is connected by a sequence of transmission lines and every capital is directly connected to only one city.

The first line of the input contains two integers $$$N, K$$$ ($$$4 \leq N \leq 100$$$; $$$3 \leq K < \min(10, N))$$$, indicating respectively the number of cities and the number of capitals. The following $$$N$$$ lines contain two integers $$$X$$$ and $$$Y$$$ each ($$$−1000 \leq X, Y \leq 1000$$$), representing the coordinates of a city. The $$$K$$$ first cities are the capitals. There are no two cities with the same coordinates.

Print a line containing a real number, with 5 decimal places, indicating the smallest total cost to build transmission lines, according to the restrictions above.

6 4
-20 10
-20 -10
20 10
20 -10
-10 0
10 0

76.56854

22 9
-3 -25
0 -6
-1 -9
2 -21
-5 -19
0 -23
-2 24
-4 37
-3 33
-3 -12
2 39
3 -49
-3 -26
2 24
5 3
-4 -9
-2 -9
-4 8
3 -33
-2 31
-1 -13
0 2

95.09318