405475: GYM101972 A Multiplication Dilemma

Multiplication operation is not always easy! For example, it is hard to calculate 27 × 20 using your mind, but it is easier to find the answer using the following methods: 30 × 20 - 3 × 20. It turns out that people can calculate the multiplication of two special numbers very easily.

A number is called special if it contains exactly one non-zero digit at the beginning (i.e. the most significant digit), followed by a non-negative number of zeros. For example, 30, 7, 5000 are special numbers, while 0, 11, 8070 are not.

In this problem, you are given two numbers a and b. Your task is to calculate the multiplication of a and b (a × b), by writing the multiplication expression as a summation or subtraction of multiplication of special numbers. Can you?

The first line contains an integer T (1 ≤ T ≤ 10⁴) specifying the number of test cases.

Each test case consists of a single line containing two integers a and b ( - 10⁹ ≤ a, b ≤ 10⁹, a ≠ 0, b ≠ 0), as described in the problem statement above.

For each test case, print a single line containing the multiplication expression of a and b as a summation or subtraction of multiplication of special numbers. All special numbers must be between  - 10⁹ and 10⁹ (inclusive). If there are multiple solutions, print any of them. It is guaranteed that an answer always exists for the given input.

The multiplication expression must be printed in exactly one line. A single term must be printed as 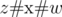in which z and w are both special numbers, # represents a single space, and x represents the multiplication operation. Two consecutive terms must be printed as 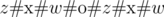in which z and w are both special numbers, # represents a single space, represents the multiplication operation, and represents either the addition operation  +  or the subtraction operation  - . (Check the sample output for more clarification).

2
55 20
70 17

60 x 20 - 5 x 20
-3 x 70 + 70 x 20