405595: GYM102006 H Bugged System
Description
Mr. Light is visiting a city with a "smart" metro system. Or so it seems ...
There are exactly n stations in a line, where the ith station is located at a distance xi from the beginning of the line. You can check into some station, travel between the stations as many times as you want in both directions, and check out from another station. The metro card will track the sum of distances you traveled and charge you accordingly once you check out of your destination station.
However, there seems to be a bug in the system; if you happen to check in and out from the same station, you will be charged 0 credit. This creates the possibility of a scenario where one person traveling from stations a to b, and another person traveling from stations b to a, they can now meet up at some station and swap their cards. Therefore when they arrive, they both will pay 0 credit. Check the explanation of the first sample test for another scenario.
A person can go to any number of stations and wait as long as they like. Two people that meet at the same station can swap their cards.
You are given the starting and destination stations for m people traveling along the metro. Is it possible for all m people to check out from their destination stations and pay 0 credit? If so, print the minimum total distance they must travel to achieve this.
InputThe first line of input contains a single integer T (1 ≤ T ≤ 3700), the number of test cases.
The first line of each test case contains two space-separated integers n and m (2 ≤ n, m ≤ 2 × 105), the number of stations and the number of people that will be using the metro stations.
The second line contains n 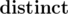 space-separated integers x1, x2, ..., xn (0 ≤ xi ≤ 2 × 106), where xi is the distance of the ith station from the beginning of the line.
space-separated integers x1, x2, ..., xn (0 ≤ xi ≤ 2 × 106), where xi is the distance of the ith station from the beginning of the line.
Each of the following m lines contains two integers si and di (1 ≤ si, di ≤ n, si ≠ di), representing the starting and destination stations of ith person.
The sum of n over all test cases doesn't exceed 2 × 106, the same is true for m.
OutputFor each test case, output on a single line with the minimum total distance all m people need to travel to pay 0 credit.
If it is not possible, output - 1 on a line.
ExampleInput2Output
3 3
10 50 25
1 2
2 3
3 1
4 2
1 10 5 3
1 2
4 3
80Note
-1
First sample explanation:
There are three metro cards, checked in at stations s1, s2, and s3 and with person p1, p2, and p3, respectively.
Person p1 goes to station s2, and swaps cards with person p2. Now person p1 can check out from station s2 with 0 credit (distance traveled 40).
Person p2 now has the card that was checked in from station s1 and goes to station s3 with it. He swaps that card with person p3 and checks out from station s3 with the new card he has (distance traveled 25).
Person p3 now goes to station s1 with the card that was also checked in from station s1 and checks out there with 0 credit (distance traveled 15).
Sum of traveled distances is 40 + 25 + 15 = 80.