405640: GYM102020 G Gabrielmetry

Pedro and Lucas are two brothers who look extremely alike in many ways, despite not being twins. One day, their friends Gabriel Mendes and Gabriel Pessoa decided to know, once and for all, if they really looked that similar, and, for that, they asked for the brothers to go for a walk on the park. They will walk the same total distance, but doing random moves. Therefore, in order to actually know the path traveled by them, Pedro and Lucas need to write their positions on every change of direction they make, or simply mark their current position whenever they wanted, until they decided to stop.

Mendes and Pessoa now decided to analyze the trajectory that was created by the movements of each of the brothers, and the result was really impressive!

Let us call each of the $$$N$$$ points marked by Pedro as $$$P_{i}$$$, and the $$$M$$$ points marked by Lucas as $$$L_{i}$$$. They verified that for each two consecutive points on each of the brothers' path (i.e. the segments $$$[P_{i}, P_{i + 1}]$$$ and $$$[L_{i}, L_{i + 1}]$$$), the distance between them were equal. That is,

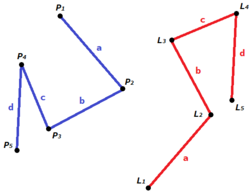
That also implied that the brothers actually marked the same number ($$$K$$$) of points. How crazy is that?

Mendes and Pessoa were so impressed that they thought:

Your goal is to print the minimum number of points that would need to be marked on the path of each one of the Gabriels (Mendes and Pessoa), so that every distance between consecutive points on their paths would be exactly the same.

The first line of input consists of two integers $$$N$$$ and $$$M$$$, $$$[2 \leq N, M \leq 20\,000]$$$, that represent, respectively:

$$${\: \displaystyle \bullet \:}$$$ The number of points marked by Mendes;

$$${\: \displaystyle \bullet \:}$$$ The number of points marked by Pessoa;

The following $$$N$$$ lines contain the points $$$P_{i}$$$ marked by Mendes $$$[-10^{9} \leq x_{P_{i}}, y_{P_{i}} \leq 10^{9}]$$$;

A blank line separates the lists of points of Mendes and Pessoa;

Then, the next $$$M$$$ lines contain the points $$$Q_{i}$$$ marked by Pessoa $$$[-10^{9} \leq x_{Q_{i}}, y_{Q_{i}} \leq 10^{9}]$$$;

The output consists of one integer: The minimum number of points that need to be added on Mendes' path and Pessoas' path.

5 3
0 0
3 0
3 4
6 4
6 8

0 0
6 8
10 8

2

- The points coordinates may not be integers;

- Two distances can be considered equal if $$$abs(D_{a} - D_{b}) \leq 10^{-5}$$$;

- The length of each segment must be equal in both paths.