405662: GYM102028 C Supreme Command

Lewis likes playing chess. Now he has $$$n$$$ rooks on the chessboard with $$$n$$$ rows and $$$n$$$ columns. All rows of the chessboard are labelled with $$$1$$$ through $$$n$$$ from top to bottom. All columns of the chessboard are labelled with $$$1$$$ through $$$n$$$ from left to right. All rooks are labelled with $$$1$$$ through $$$n$$$ as well. At the very beginning, each row or column contains exactly one rook. However, Lewis allows a square with two or more rooks during the game.

Now he starts to play a game named Supreme Command. He will provide several supreme commands to all rooks. All possible commands are in the following four different formats.

• L k: Every rook moves $$$k$$$ squares to the left;
• R k: Every rook moves $$$k$$$ squares to the right;
• U k: Every rook moves $$$k$$$ squares upward;
• D k: Every rook moves $$$k$$$ squares downward.

For a Supreme Command with given number $$$k$$$, if a rook, after moving less than $$$k$$$ squares, had arrived at a boundary (which locates in the left-most columns, right-most column, top row or bottom row) such that the rook cannot move further, it would stay there and not move outside the chessboard.

He will also have several queries about rooks. The only two possible formats about queries are listed as follows.

• ? k: Ask the current position of the $$$k$$$-th rook;
• !: Ask how many pairs of rooks there are currently located in the same square.

Your task in this problem is to answer these queries correctly.

The input contains several test cases, and the first line contains a positive integer $$$T$$$ indicating the number of test cases which is up to $$$1000$$$.

For each test case, the first line contains two integers $$$n$$$ which is described as above, and $$$m$$$ indicating the total number of supreme commands and queries, where $$$1 \leq n, m \leq 3 \times 10^5$$$.

Each of the following $$$n$$$ lines contains two integers $$$x$$$ and $$$y$$$, describing a rook located at the intersection of the $$$x$$$-th row and the $$$y$$$-th column, where $$$1 \leq x, y \leq n$$$.

Then the following $$$m$$$ lines describe all Supreme Commands and queries in chronological order, where all given parameters $$$k$$$ are integers ranged from $$$1$$$ to $$$n$$$.

We guarantee that the sum of $$$n$$$ and the sum of $$$m$$$ in all test cases are up to $$$10^6$$$ respectively.

For each test case, output several lines to answer all queries.

For each query of the first type ("? $$$k$$$"), output a line containing two integers $$$x$$$ and $$$y$$$, which indicate the current position of the $$$k$$$-th rook is the intersection of the $$$x$$$-th row and the $$$y$$$-th column. You should output exactly one whitespace between these two numbers.

For each query of the second type ("!"), output a line containing an integer which indicates the number of pairs of rocks that are currently located in the same square.

1
4 9
3 4
2 1
4 2
1 3
L 2
? 1
? 2
R 1
? 1
? 3
!
U 3
!

3 2
2 1
3 3
4 2
0
3

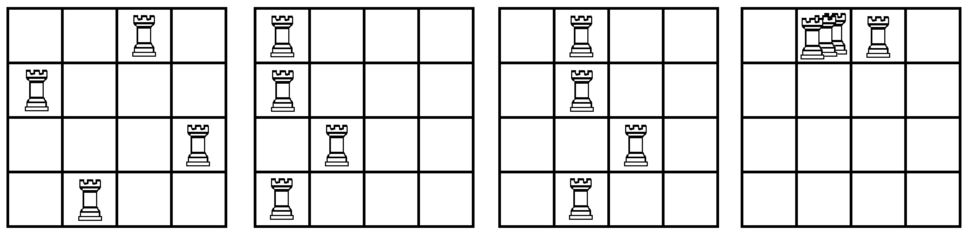
The following figures illustrate the chessboard at the beginning and after each Supreme Commands in the sample case.