405851: GYM102135 D Friends rescue

Once, during the evening walk through the forest, the boy Vova came to the river and saw that his friend Vanya was stuck on the other shore. Vova needs to save his friend, because he can not swim! There are n × (n + 1) islands in the river in the form of a grid. However, there are no bridges between them! There on the shore Vova met an evil wizard Zedikus, who agreed to help him only if Vova solves one difficult task. Vova needs to calculate the number of ways to build bridges so that there is at least one way from one shore to another. Help Vova solve this problem. Vova is allowed to build bridges only between neighboring islands.

More formally, each island has coordinates (r, c) (1 ≤ r ≤ n, 1 ≤ c ≤ n + 1), where r is the line number, and c — column number. If the island has coordinates (r, c), then the neighboring islands have coordinates (r + 1, c), (r, c + 1), (r - 1, c), (r, c - 1), if any exist. The islands that are in the first and last column, that is the islands with coordinates (r, c), where 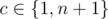(that is, c is equal to either 1, or n + 1), are already connected to the shores.

The way from one shore to another is a sequence of islands (r₁, c₁), (r₂, c₂), ..., (r_k, c_k) such that for each i (1 ≤ i < k) there is a bridge between the islands (r_i, c_i) and (r_i + 1, c_i + 1), also the island (r₁, c₁) is in the first column (c₁ = 1), and the island (r_k, c_k) is in the last column (c_k = n + 1).

Two ways to build bridges are considered different if there is such a bridge that in one way it is built, and in another there is not. For a better understanding, see the illustration of one way to build bridges.

You can see two shores described in the problem statement on the picture. The left shore is denoted as L, and the right one as R. Green circles depict the islands. Rounded rectangles depict the bridges. As can be seen, the shown bridge configuration contains the path between the left and the right shores. As a reminder, the bridges between the left shore L and the left column of the islands are present initially. Same thing goes for the right bank R and the right column of islands. rows and columns arrows correspond to the coordinate axes for rows and columns

The only line of input contains a single integer n (1 ≤ n ≤ 42) — the dimension of the grid of islands.

Output a single integer — the answer to the task modulo 10⁹ + 7.

1

1

42

37237670