405854: GYM102135 G Digital characteristic

The digital characteristic of number n is a function f(n) such that:

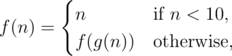
where g(n) — the sum of the digits of the decimal representation of a number n.

Vanya has already learned how to quickly calculate a digital characteristic for significantly large numbers in the mind, so he decided to show this skill to all participants of the BSUIR Open 2018. The participants didn't really like his bragging, so they offered him to calculate the digital characteristic for a very large number. The number was so huge that it was impossible to write it down on a paper.

Instead of the number itself, Vanya received its description which could help him to restore this number. Description consists of four numbers a, b, m and k. To get the initial number, Vanya must first generate k numbers a_i such that 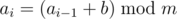for i > 1, . The received numbers he must write on a piece of paper in the reversed order, thus having received one large number. Finally he must find a digital characteristic for this number.

Now it remains to learn how to check the answer. Write a program that will determine the digital characteristic according to a given description of the number.

The first line contains an integer t (1 ≤ t ≤ 10 000) — an amount of numbers, for which is needed to calculate digital characteristic.

Each of the next t lines contains description of a number. Each description consists of four integers a, b, m and k (0 ≤ a, b ≤ 10⁹, 2 ≤ m ≤ 10⁹ + 7, 1 ≤ k ≤ 10⁹) — number generation parameters.

It is guaranteed that the numbers restored from those descriptions do not contain leading zeros. Note that the 0 number does not contain leading zeros.

Print t lines. For each line print ans (0 ≤ ans ≤ 9) — digital characteristic of appropriate number.

4
1 1 10 5
4 5 7 8
1 2 3 4
42 42 2018 18

6
7
4
9

According to the first description the number is 54321. Its digital characteristic equals f(54321) = f(15) = f(6) = 6.

According to the fourth description the number is 7567146726305885465044624203783362942522101681268442.