405858: GYM102135 K A Boring Problem

While boring neighbors' children play boring football outdoors, little Jim plays with his own precious tree, which consists of exactly n vertices. Jim puts a small token onto some vertex S. Game ends as soon as the token reaches special vertex F. Obviously, to end the game token should be moved somehow (for the most dreadfully meticulous our readers it should be noted, that S and F never coincide). Any sequence of token's moves, which resembles any other sequence, which Jim saw before, is considered to be incredibly boring. To avoid incredibly boring sequences little boy moves token randomly: if token is placed on vertex v, he selects uniformly at random one of v's neighbors in the tree and places token onto it. After playing about 4↑↑ 2 times the game started to feel a little boring. On the other hand, quite big number of played games helped Jim to develop intuition about how many moves at average it takes to finish the game with given S and F. On the next day, Jim decided that experimenting on innocent people is more funny than playing with his tree. To begin with he decided to investigate how well do others perform on calculating expected number of moves to finish a game on some particular tree.

The first line of input contains two integers 2 ≤ n ≤ 10⁵ and 1 ≤ q ≤ 10⁵ — number of vertices in tree and number of pairs (S, F) for which expected number of moves should be calculated.

The next n - 1 lines contain the edges of Jim's tree. Each line contains two integers v and u (1 ≤ u_i, v_i ≤ n, u_i ≠ v_i) — endpoints of an edge. It is guaranteed that the given graph is a tree.

The next q lines contain pairs 1 ≤ S_i, F_i ≤ n (S_i ≠ F_i) — start and finish vertex in the i-th experiment.

It can be shown that for any tree with given start and finish vertices S and F the expected number of moves to finish the game can be represented as 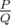, where P and Q are coprime and 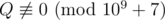. For each pair of vertices (S_i, F_i) output P × Q^- 1 modulo 10⁹ + 7 on a separate line.

3 2
1 2
2 3
1 3
1 2

4
1