406103: GYM102267 H Circle of Polygon
Description
A $$$\textbf{circumscribed circle}$$$ of a polygon is the circle that passes through all the vertices of that polygon.
Let's assume we have a $$$\textbf{regular}$$$ polygon, we want to find the area of the circumscribed circle around this polygon. Given the number of vertices and the side length of the polygon, can you find the circle's area?
The only line contains $$$2$$$ integers , $$$V(3 \le V \le 359)$$$ the number of vertices of the polygon and $$$S(1 \le S \le 10^9)$$$
OutputFind the area of the resulting circumscribed circle.Your answer will be considered correct if its absolute or relative error does not exceed $$$10^{-6}$$$.
Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if $$$\frac{|a-b|}{max(1,b)}\le 10^{-6}$$$.
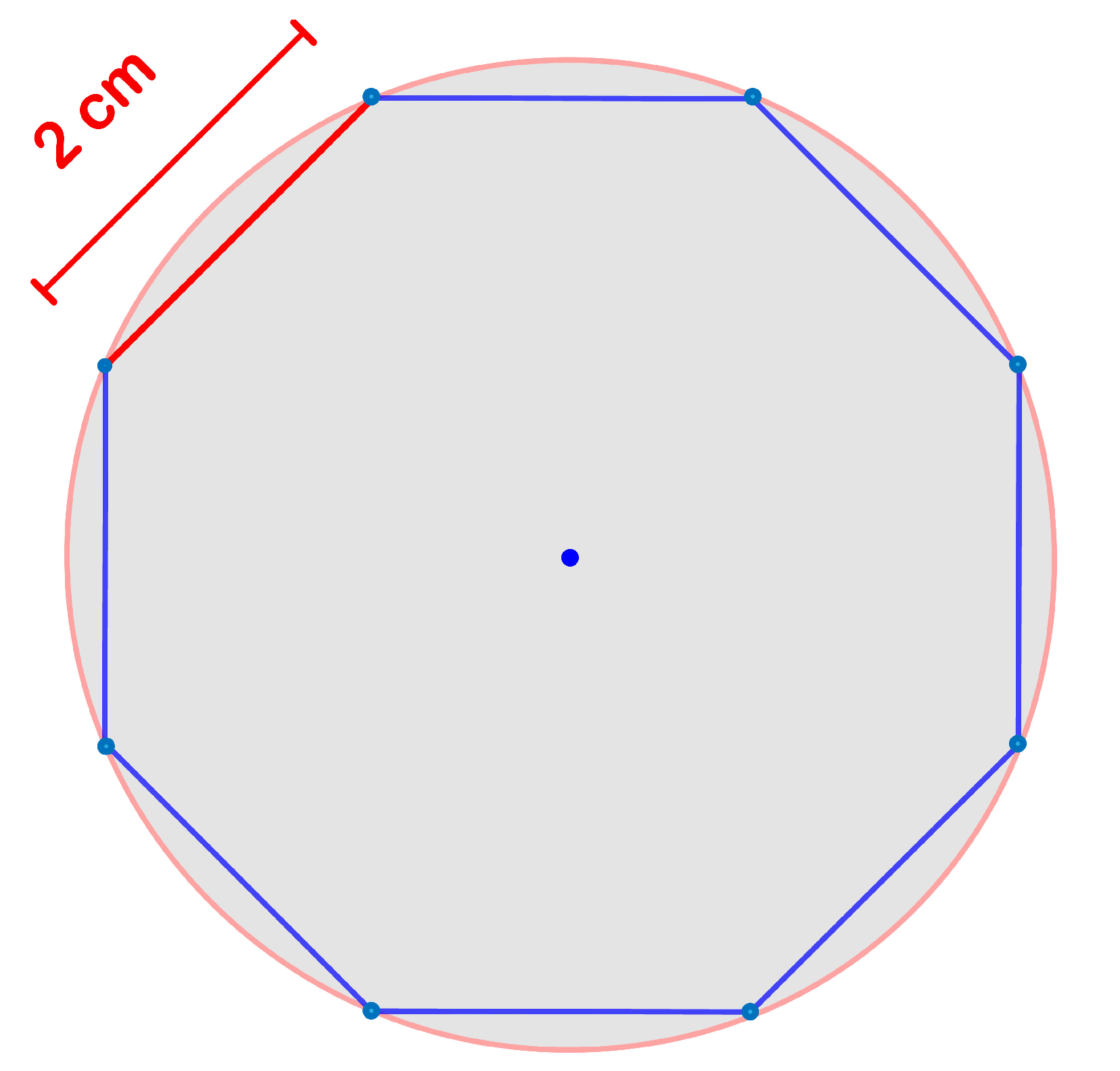
ExampleInput8 2Output
21.452136491Note
The octagon in the picture illustrates the first example.