406585: GYM102448 D Drinking to turn red
Description
After the closing ceremony of an ICPC competition, Lucas and his friend decided to go to the hotel pool to have some magical drinks. After a while, Lucas found a magic swim ring and also realized that the swim rings had some interesting properties:
- The swim rings are perfectly circular.
- The swim rings do not move.
- There may be a non-empty intersection between the swim rings in the pool.
- The magic swim ring can absorb any swim ring it intersects or is tangent to. After absorption, the radius of the magic swim ring will be equal to the sum its current radius and the radius of the swim ring that was absorbed.
Assuming the pool is an infinite plane and the swim rings are located at points ($$$X_i$$$, $$$Y_i$$$) with radius $$$R_i$$$, Lucas would like to know the smallest possible radius, such that if he places a magic swim ring centered at the point ($$$x$$$, $$$y$$$), all swim rings would be absorbed by the magic ring.
Example:
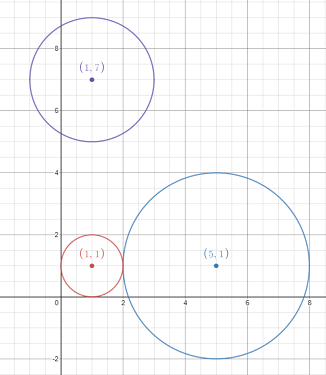
In this example, the magic swim ring (red) would need a radius of at least 1 to absorb the blue swim ring. After absorption, its new radius would be equal to 4, and then it would be able to absorb the purple swim ring.
InputThe first line of input contains three integers $$$N$$$ ($$$0 < N \le 10^5$$$) and $$$x$$$, $$$y$$$ ($$$-10^9 < x, y \le 10^9$$$), the number of swim rings and the center of the magic swim ring.
The $$$i$$$-th of the next $$$N$$$ lines contains three integers $$$X_i$$$, $$$Y_i$$$ ($$$-10^9 < X_i, Y_i \le 10^9$$$) and $$$R_i$$$($$$1 < R_i \le 10^5$$$), center and radius of the $$$i$$$-th swim ring.
OutputYou must print the minimum radius the magic swim ring should have in order to solve Lucas' challenge. Your answer is considered correct if its absolute or relative error does not exceed $$$10^{-6}$$$.
ExamplesInput2 1 1 1 7 3 5 1 3Output
1.0000000000Input
4 211 -458 335 369 6 -771 -753 30 193 -617 41 -27 -396 78Output
870.3531099090