406593: GYM102452 A Axis of Symmetry
Description
Symmetry in everyday language refers to a sense of harmonious and beautiful proportion and balance. In mathematics, "symmetry" has a more precise definition, that an object is invariant under any of various transformations; including reflection, rotation or scaling.
The axis of symmetry of a two-dimensional figure is a line such that, if a perpendicular is constructed, any two points lying on the perpendicular at equal distances from the axis of symmetry are identical. Another way to think about it is that if the shape were to be folded in half over the axis, the two halves would be identical: the two halves are each other's mirror image. Thus a square has four axes of symmetry, because there are four different ways to fold it and have the edges all match. A circle has infinitely many axes of symmetry passing through its centre, for the same reason.
In this problem, you are given $$$n$$$ rectangles with sides parallel to the coordinate axes on the 2D Cartesian plane. The area of the intersection of any two rectangles is zero. Your task is to find the axes of symmetry of the figure formed by these rectangles.
InputThe input contains multiple cases. The first line of the input contains a single integer $$$T$$$ ($$$1\leq T\leq 10^5$$$), the number of cases.
For each case, the first line of the input contains a single integer $$$n$$$ ($$$1\le n\le10^5$$$), the number of rectangles. In the following $$$n$$$ lines, the $$$i$$$-th $$$(1 \le i \le n)$$$ line contains four integers $$$x_1,y_1,x_2$$$ and $$$y_2$$$ ($$$x_1 < x_2,y_1< y_2$$$), denoting the coordinates of two opposite corners of the $$$i$$$-th rectangle $$$(x_1,y_1)$$$ and $$$(x_2,y_2)$$$.
It is guaranteed that the sum of $$$n$$$ over all cases does not exceed $$$10^5$$$ and the absolute value of all coordinates do not exceed $$$100\,000\,007$$$.
OutputFor each case, print a single integer $$$m$$$, the number of axes, on the first line of the output. Then print $$$3m$$$ space-separated integers $$$s_0, s_1,\cdots, s_{3m-1}$$$ on the second line, where $$$\gcd(s_{3i},s_{3i+1},s_{3i+2})=1$$$ for all $$$0 \le i < m$$$, denoting that the $$$(i+1)$$$-th axis of symmetry is $$$s_{3i}\cdot x+s_{3i+1}\cdot y=s_{3i+2}$$$. Note that $$$\gcd(a,b,c)$$$ denotes the greatest common divisor of $$$a,b,c$$$.
If there are multiple solutions, you need to print the lexicographically largest solution. A solution $$$\{s_i\}_{i=0}^{3m-1}$$$ is lexicographically larger than $$$\{t_i\}_{i=0}^{3m-1}$$$ if and only if there is some $$$j\ (0\leq j<3m)$$$ such that $$$s_j>t_j$$$ and $$$s_i=t_i$$$ for any $$$0 \le i<j$$$.
ExampleInput3 2 -1 -1 0 1 0 0 1 2 2 -1 -1 0 0 0 0 1 1 3 -1 -1 0 1 0 -1 1 0 0 0 1 1Output
0 2 1 1 0 1 -1 0 4 1 1 0 1 0 0 1 -1 0 0 1 0Note
The following figures illustrate the third sample case.
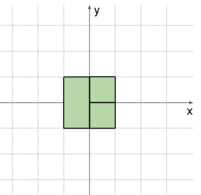 The rectangles in the third sample case.
The rectangles in the third sample case. 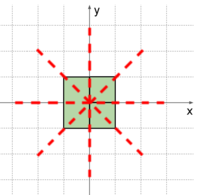 All axes in the third sample case.
All axes in the third sample case.