406709: GYM102503 F Ulam Spiral
Description
In the heart of the city, there is an infinite set of ulams. The ulams are indexed by positive integers. For any positive integer $$$a$$$, ulam $$$a$$$ can feed $$$a$$$ persons. The ulams are positioned in an infinite two dimensional grid like so:
17 16 15 14 13
18 5 4 3 12
19 6 1 2 11
20 7 8 9 10
21 22 23 24 25 ...
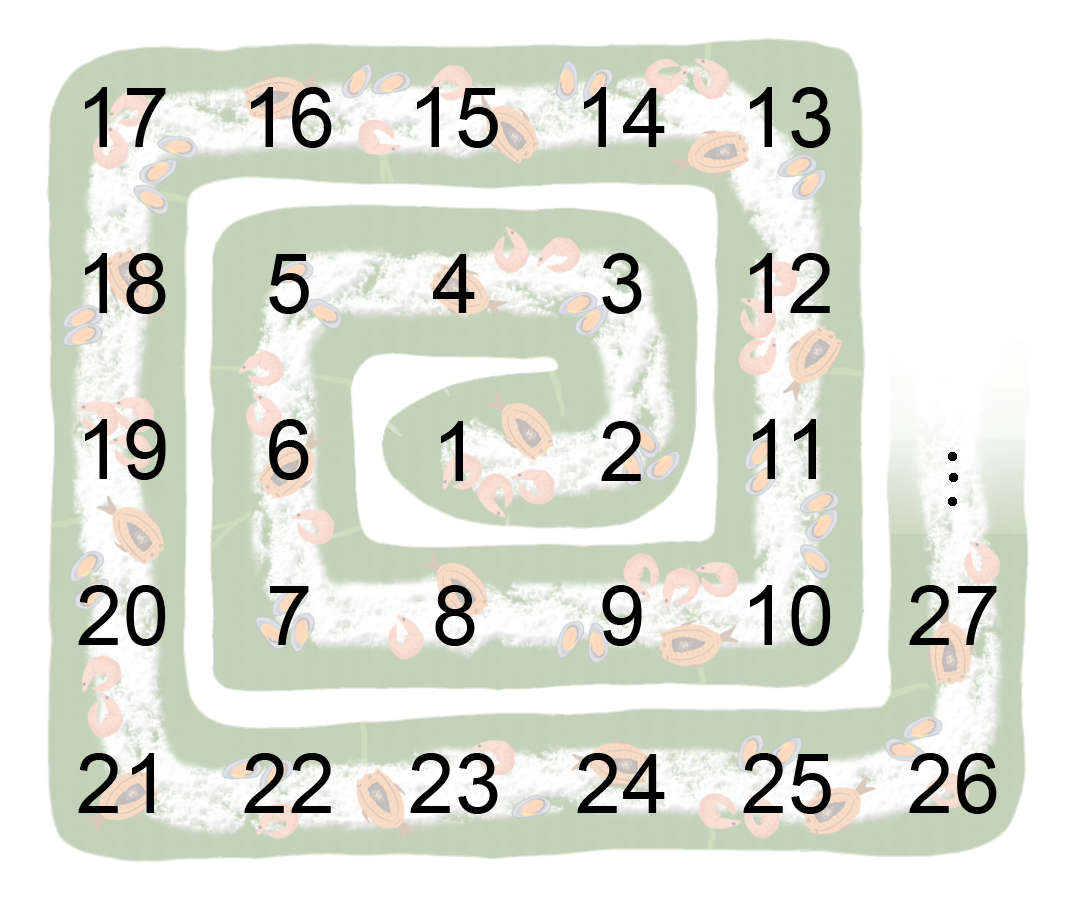
One may wonder why they are positioned like this. It is because according to a popular Filipino song: kung ulam sa puso ay tunay ngang gan'yan.
This problem will be about subrectangles of this ulam spiral. Suppose Ulam $$$69420$$$ is on cell $$$(0, 0)$$$. A cell which is $$$a$$$ cells up and $$$b$$$ cells right of Ulam $$$69420$$$ is called cell $$$(a, b)$$$.
The subrectangle $$$R_{w,x,y,z}$$$ is the set of cells whose coordinates $$$(a, b)$$$ satisfy $$$w \leq a \leq x$$$ and $$$y \leq b \leq z$$$. One could notice that the four corners of the subrectangle $$$R_{w,x,y,z}$$$ are $$$(w, y)$$$, $$$(w, z)$$$, $$$(x, y)$$$, and $$$(x, z)$$$. The size of a subrectangle is defined to be the number of cells contained in it. We say that subrectangle $$$R_{w,x,y,z}$$$ contains ulam $$$i$$$ if ulam $$$i$$$ is on a cell contained in $$$R_{w,x,y,z}$$$.
Given two positive integers $$$i$$$ and $$$j$$$, your task is to figure out the smallest subrectangle $$$R$$$ containing ulams $$$i$$$ and $$$j$$$, and find how many people the ulams contained in $$$R$$$ can feed.
The answer may be very large. Output the answer modulo $$$10^9 + 7$$$.
InputThe first line of input contains $$$t$$$, the number of test cases.
Each test case consists of a single line containing two space-separated integers $$$i$$$ and $$$j$$$.
OutputFor each test case, output a single line containing a single integer denoting the answer for that test case.
Scoring$$$1 \le t \le 20000$$$
$$$1 \le i, j \le 10^{18}$$$
Subtask 1 (25 points):
$$$i, j \le 50$$$
Subtask 2 (20 points):
$$$i, j \le 10^6$$$
Subtask 3 (18 points):
$$$i, j \le 10^9$$$
Subtask 4 (11 points):
$$$i, j \le 10^{12}$$$
Subtask 5 (11 points):
$$$t \le 4000$$$
$$$|i - j| \le 16$$$
Subtask 6 (9 points):
$$$t \le 4000$$$
$$$|i - j| \le 5000$$$
Subtask 7 (6 points):
No additional constraints.
ExampleInput3 2 12 9 7 7 9Output
28 24 24