406732: GYM102512 A Leakage

Makoto told his friend, Sekai, who he secretly likes. However, it turned out to be a terrible idea, as she couldn't keep a secret and the information got spread around the class, eventually reaching the girl he likes. He is really angry at the situation, but what's done cannot be undone. To hopefully prevent anyone else from facing the same awkward situation, he decides to analyze this phenomenon.

Makoto has $$$N$$$ classmates, $$$M$$$ pairs of which are friends (friendship is mutual). It is guaranteed that for any two classmates $$$X$$$ and $$$Y$$$ there exist a chain of classmates $$$A_1, A_2,..., A_m$$$ such that the pairs $$$(X, A_{1}),(A_1, A_2),...,(A_{m-1}, A_m),(A_m, Y)$$$ are friends.

All of the $$$N$$$ classmates like to gossip. Hence, if one of these classmates receive some information, they will tell it to all their friends.

Makoto imagines $$$Q$$$ scenarios. Suppose classmate $$$C_i$$$ receives a message, and the message is not supposed to reach classmate $$$D_i$$$. He can bribe exactly one of these $$$N$$$ classmates (except classmate $$$C_i$$$ and $$$D_i$$$) to not spill his secret. He wants to know the number of people he can bribe to prevent the message from spreading to person $$$D_i$$$.

The first line of input contains two space-separated integers, $$$N, M$$$ ($$$3 \le N \le 200000, 1 \le M \le 200000$$$).

The next $$$M$$$ lines of input contain two space-separated integers each, $$$u, v$$$ ($$$1 \le u, v \le N, u \neq v$$$), denoting that classmates $$$u$$$ and $$$v$$$ are friends. It is guaranteed that no pair of classmates appear twice in the input, and for any two classmates $$$X$$$ and $$$Y$$$ there exist a chain of classmates $$$A_1, A_2,..., A_m$$$ such that the pairs $$$(X, A_{1}), (A_1, A_2), ..., (A_{m-1}, A_m), (A_m, Y)$$$ are friends.

The next line contains a single integer $$$Q$$$ ($$$1 \le Q \le 200000$$$), denoting the number of scenarios.

The next $$$Q$$$ lines of input contain two space-separated integers each, $$$C_{i}, D_{i}$$$ ($$$1 \le C_{i}, D_{i} \le N, C_{i} \neq D_{i}$$$), describing a scenario.

For each of the $$$Q$$$ scenarios, output a line containing a single integer, denoting the number of possible classmates Makoto can bribe to prevent the message from spreading from classmate $$$C_{i}$$$ to classmate $$$D_{i}$$$.

Subtask 1 (11 points): $$$N, M, Q \le 300$$$

Subtask 2 (20 points): $$$M = N - 1$$$

Subtask 3 (69 points): No additional constraints

9 14
1 2
1 3
3 4
3 5
4 5
4 7
5 6
5 7
6 7
1 8
1 9
2 9
2 8
9 8
3
3 8
1 3
4 9

1
0
2

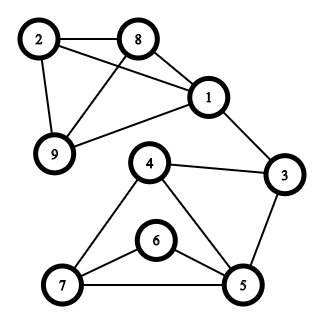
This is how the friendship network looks like for the sample testcase.

In the first scenario, the only way to prevent the message from spreading from classmate $$$3$$$ to classmate $$$8$$$ is to bribe classmate $$$1$$$.

In the second scenario, there is no way to prevent the message from spreading from classmate $$$1$$$ to classmate $$$3$$$ since they are already friends (note that you can't bribe either of them).

In the third scenario, there are $$$2$$$ possible ways to prevent the message from spreading from classmate $$$4$$$ to classmate $$$9$$$: bribing classmate $$$1$$$ or classmate $$$3$$$.