406962: GYM102625 H Ye Wali Meri Hai!!

H. Ye Wali Meri Hai!!time limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard output

Assuming, Geek has become the new sexy, The ultimate geeks of the class of 2020 (with high packages) decided to come up with an algorithm which can find the list of girls who would be their potential gfs/bfs (Some Boys might be interested in other boys). Due to limited time, They decided to find the girl with the maximum beauty.

Now, there is a problem, The coders follow the BroCode which clearly states that "A Bro can't try on a girl , another bro is trying on "

According to the algo, All the students can be represented as a tree rooted at node $$$1$$$ with the nodes being the students and the weights their beauty such that the subtree of each boy is the list of potential gfs/bfs.

Note: The subtree of one bro can contain the subtree of other bros

When queried for a Bro, The algo returns the beauty of the most beautiful individual in his subtree. As the Bros have taken an oath to follow the BroCode, For each query, they want to modify the algo in such a way that if a set of other Bros nodes are also given and the algo has to return the beauty of the most beautiful individual excluding the subsequent bros subtree and $$$s_1$$$ himself.

To sum up, A tree rooted at $$$1$$$ of $$$n$$$ nodes is given. there are $$$q$$$ queries such that for each query, a set of numbers from $$$1$$$ to $$$n$$$ is provided. The algo must print the maximum weight in the subtree of first number $$$s_1$$$ excluding the nodes in the subtree of other numbers $$$s_2$$$ onwards.

Input

The first line consists of two integers $$$n$$$(no. of nodes) and $$$q$$$(no. of queries) (1 $$$\leq$$$ $$$n$$$, $$$q$$$ $$$\leq$$$ $$$10^5$$$)

The second line contains $$$n$$$ integers $$$a_1$$$...$$$a_n$$$, where $$$a_i$$$ is the beauty of the $$${i^{th}}$$$ node (0 $$$\leq$$$ $$$a_i$$$ $$$\leq$$$ $$$10^9$$$)

The next $$$n$$$-1 lines contain two integers $$$u$$$ and $$$v$$$ indicating that there lies an edge between $$$u$$$ and $$$v$$$ (1 $$$\leq$$$ $$$u$$$, $$$v$$$ $$$\leq$$$ $$$n$$$)

The next $$$q$$$ lines consists of an integer $$$k$$$ and then $$$k$$$ pairwise distinct integers $$$s_1$$$...$$$s_k$$$ (1 $$$\leq$$$ $$$s_i$$$ $$$\leq$$$ $$$n$$$)

The sum of $$$k$$$ over all queries won't exceed $$$10^5$$$

Output

Output consists of $$$q$$$ lines corresponding to the maximum beauty in the subtree of $$$s_1$$$ excluding the subtrees of $$$s_2$$$... $$$s_k$$$ per query

Print $$$-1$$$ if $$$s_1$$$ itself lies in the subtree of any of $$$s_2$$$...$$$s_k$$$ or excluding $$$s_1$$$ the subtree is empty.

ExampleInput

8 4
2 20 4 5 4 10 4 8
1 2
1 3
3 4
4 7
4 8
2 5
2 6
1 4
3 4 1 8
3 4 2 6
2 1 2

Output

8
-1
8
8

Note We can imagine it directed tree with the nodes below including the node itself form its sub-tree.

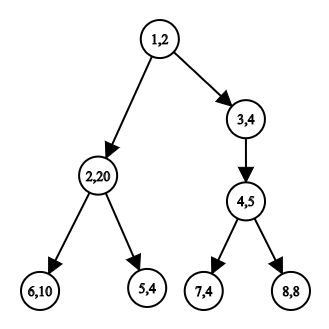
In first query,only one input is given, answer= max($$$4$$$,$$$8$$$) = $$$8$$$

In the second query, $$$4$$$ lies in the sub-tree of $$$1$$$ , answer = $$$-1$$$

In the third query, $$$2$$$ and $$$6$$$ aren't a part of the sub-tree of $$$4$$$, so they have no effect on the answer, so answer = max( $$$4$$$,$$$8$$$ ) = $$$8$$$

In the fourth query, $$$2$$$ is a part of sub-tree of $$$1$$$ , so answer excludes the sub-tree of 2, answer= max($$$2$$$, $$$4$$$, $$$5$$$, $$$4$$$, $$$8$$$) = $$$8$$$