406981: GYM102644 I Count Paths Queries

You are given a graph with $$$n$$$ vertices (numbered $$$1$$$ through $$$n$$$) and $$$m$$$ directed edges.

You need to answer $$$q$$$ queries: given $$$s, t, k$$$, count paths consisting of $$$k$$$ steps (edges) from vertex $$$s$$$ to vertex $$$t$$$, modulo $$$10^9+7$$$. A path can visit the same vertex or edge multiple times.

The first line contains three integers $$$n$$$, $$$m$$$ and $$$q$$$ ($$$1 \leq n, q \leq 200$$$, $$$0 \leq m \leq n \cdot (n - 1)$$$) — respectively the number of vertices, edges and queries.

The following $$$m$$$ lines describe edges. The $$$i$$$-th of these lines contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \leq a_i, b_i \leq n, a_i \neq b_i$$$), denoting a directed edge from $$$a_i$$$ to $$$b_i$$$. There are no self-loops or multiple edges.

The following $$$q$$$ lines describe queries. Each line contains three integers $$$s$$$, $$$t$$$ and $$$k$$$ ($$$1 \leq s, t \leq n$$$, $$$1 \leq k \leq 10^9$$$) — the start and end of a path, and its length in edges.

For each query, print a line with the answer modulo $$$1000000007$$$.

3 4 4
1 2
2 3
3 1
2 1
1 2 6
3 3 5
1 3 1
3 2 54

2
1
0
922111

In the first sample test, we are given the following graph with $$$n = 3$$$ vertices and $$$m = 4$$$ edges.

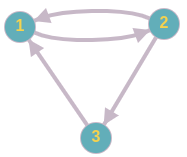
In the first query, there are 2 paths of length $$$k = 6$$$ from vertex $$$1$$$ to vertex $$$2$$$:

• $$$1 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 2 \rightarrow 1 \rightarrow 2$$$
• $$$1 \rightarrow 2 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 1 \rightarrow 2$$$