407161: GYM102697 132 Code RAMs

You have a function $$$f(x)$$$, and you want to figure out how the area under $$$f(x)$$$ from 0 to $$$C$$$.

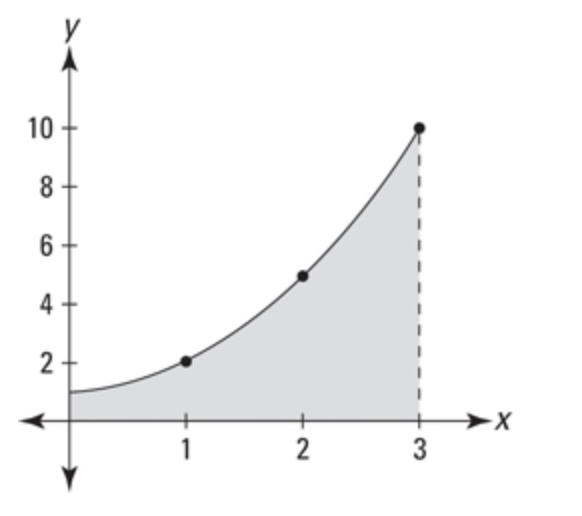
In calculus, this value is called the $$$integral$$$ of $$$f(x)$$$. For some functions, taking its integral is relatively easy and uses a few simple rules. However, for many functions, it is impossible to find their integral exactly. However, you can make an approximation of the integral, and since you're writing a computer program, you can make a close approximation.

One way to approximate the integral of a function is to use the Rectangular Approximation Method, or RAM. This method approximates the function $$$f(x)$$$ as $$$n$$$ rectangles, each having an equal width, and having varying $$$y$$$-values depending on the value of $$$f(x)$$$ at that point.

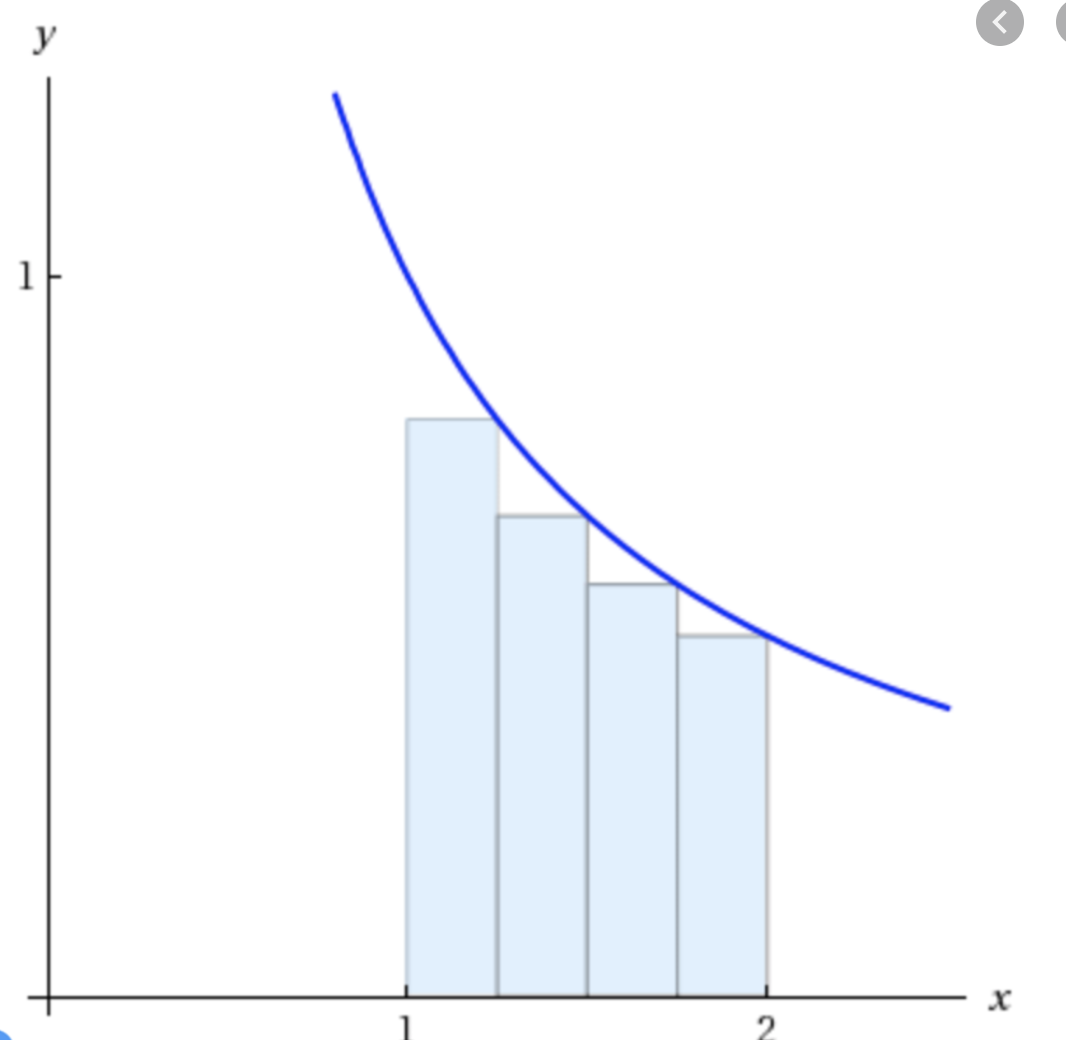
As you can see, the example with $$$n$$$=4 ($$$f(x)$$$ was divided into four rectangles) was not perfect. However, as $$$n$$$ gets larger and larger, the approximations get more and more accurate.

Formally, define the LRAM (Left Rectangular Approximation Method) approximation of the area under a function $$$f(x)$$$ from $$$0$$$ to $$$C$$$, using $$$n$$$ rectangles, as A, and the area of each rectangle as A1, A2 ... AN, as the following:

A = $$$\frac{A1 * C}{N}$$$ + $$$\frac{A2 * C}{N}$$$ + $$$\frac{A3 * C}{N} $$$+ ... + $$$\frac{AN * C}{N}$$$.

The area of each rectangle can be calculated using the standard formula A = $$$l$$$ x $$$w$$$. The width of each subrectangle is equal to $$$\frac{C}{n}$$$ (because there are $$$n$$$ rectangles with a total width of $$$C$$$). The length of each subrectangle is equal to $$$f(\frac{k * c}{n})$$$, where $$$k$$$ represents the index of the rectangle, ranging from $$$0$$$ to $$$n - 1$$$, inclusive.

Since your answer must be a relatively close approximation, but your program should fit inside of the 10 second time limit (longer than usual for this problem), you should set $$$N$$$ equal to 50000.

The only line of input contains a calculus equation. The equation will consist of the variable $$$x$$$, exponents, parentheses, and multiplication, division, addition, and subtraction operations. For example, $$$\frac{x^2 - 3}{x^3 - x + 5}$$$ would be a valid input, but $$$cos(x)$$$ would be not.

Output a single decimal number: the area under $$$f(x)$$$ from $$$x$$$=$$$0$$$ to $$$x$$$=$$$C$$$. Your number should be close to the actual answer, but it doesn't have to be exact. Using eval() or similar commands in your program is not allowed.

x^3 + x^2
2

6.666426668800027

(x^2 + x + 3) / (x^3 + x^2 + 5x)
7

0.9806709605550483

x^2
5

41.66541667500017

In the first sample case, $$$6.663$$$ would be judged as correct, but $$$7$$$ would be judged as incorrect.