407206: GYM102697 177 Ken Ken Solver
Description
Ken Ken is a number puzzle created in 2004 by Tetsuya Miyamoto.
Like Sudoku, Ken Ken involves placing numbers into an n by n grid, and it requires each row and column to contain distinct integers from 1 to n. n can range from 4 to 7, inclusive.
Additionally, each of the n * n cells in the Ken Ken puzzle is assigned to a "cage" consisting of one or more cells. If a cage consists of multiple cells, they have to form a single block of cells connected vertically or horizontally, but not diagonally. For example, an L-shaped cage, or a 2 by 2 square cage would be valid, but a cage consisting only of two cells at the opposite end of the board would not be valid. Usually, cages don't have more than 4-5 cells (although there is no upper limit).
For each cage in the puzzle, if it consists of only one cell, the cage will simply be assigned a number, indicating which number is placed in the cage in the final solution. This is called a "freebie".
Otherwise, each cage with two or more cells is assigned a math operation. All of the cells in the cages must complete the math operation successfully. For example, if a cage had the operation "9+", the total sum of the numbers in the cells of the cage would have to sum to 9. If a cage had the operation "120x", the total product of the numbers in the cage would have to be 120.
Cages can also have subtraction or division operations. These types of cages have to have exactly two cells. For subtraction, the difference of the two numbers in the cage must equal the given number. For example, if a cage had the operation "2-", then the numbers could be 3 and 1, in any order. They could also be 4 and 2, 2 and 4, 5 and 3 (if the board was at least 5 by 5), and so on. Cages with division work similarly. The number in the cage must equal the quotient of the higher number divided by the lower number. For example, for a "2/" cage, the numbers could be 1 and 2, or 2 and 1, or 4 and 2, and so on. As such, the required number of a cage will always be a positive integer.
Note that although all rows and columns must consist of distinct numbers, cages do not have to.
Here's an example of what an unsolved Ken Ken puzzle looks like:
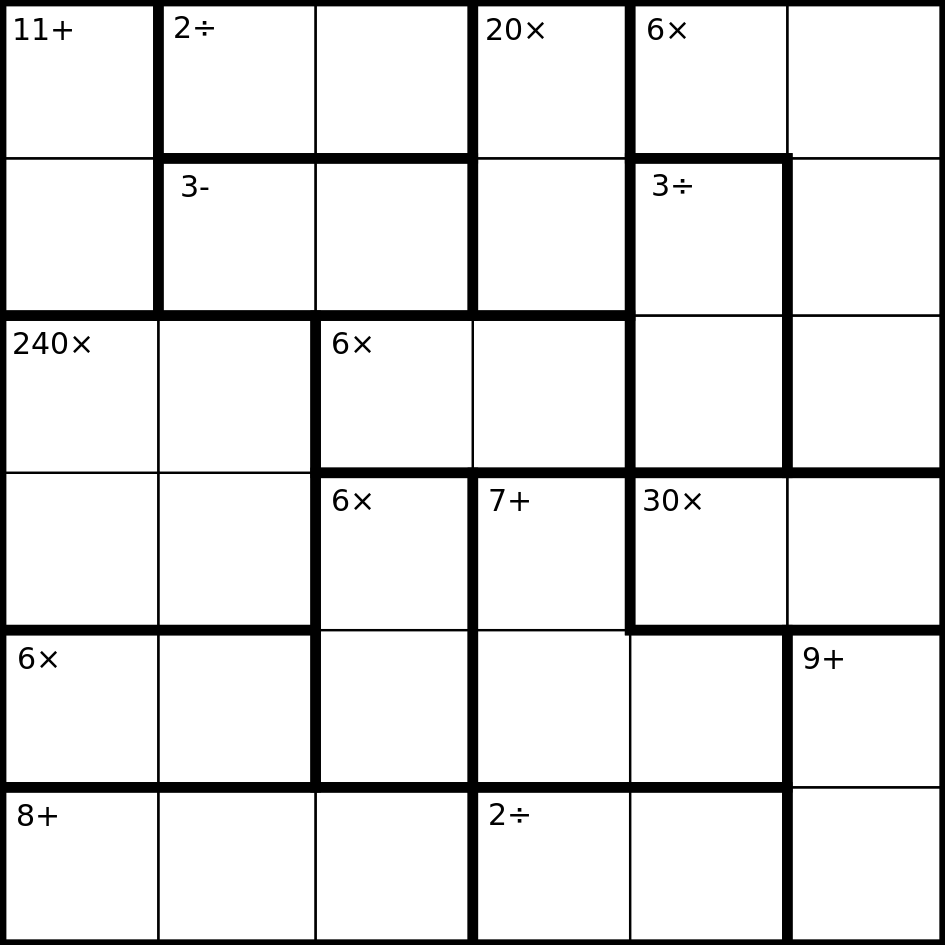
And here's the solution to the same Ken Ken puzzle:
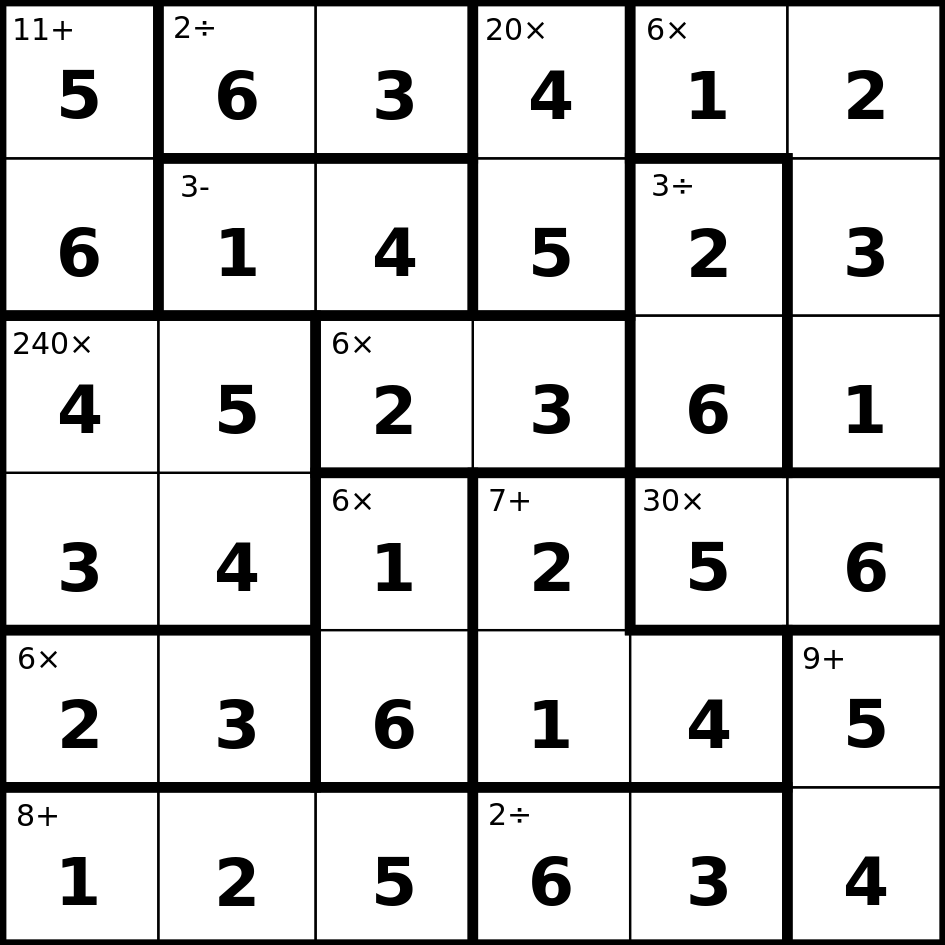
Your task, as you might have guessed, is to write a program to solve a Ken Ken puzzle. All of the Ken Ken puzzles will range from 4 by 4 to 7 by 7 in size, and they will all be taken from a book of Ken Ken puzzles, meaning that they will all be potentially solvable by a human.
Good luck!
InputThe first line of input consists of a single positive integer $$$n$$$: representing the size of the Ken Ken puzzle (the puzzle will be an $$$n$$$ by $$$n$$$ puzzle). $$$n$$$ will be less than or equal to 7 for this problem.
The next lines will contain a grid representation of the Ken Ken puzzle. Each cage will be marked off with pipes ("|") and hyphens ("-"). See the example cases for the exact formatting of the input.
The cell in each cage closest to the top of the puzzle will contain the math operation. If two cells in a cage are the same distance from the top of the puzzle, the leftmost one will contain the math operation.
OutputOutput $$$n$$$ lines, each consisting of $$$n$$$ integers: the solution to the Ken Ken puzzle.
ExamplesInput5 |---|---|---|---|---| |40x |2- | | | | |---|---|---|---|---| |8+ |24x |8+ | | | | | | |---|---|---| | | |8+ | | | | | | |---|---| |---|---| |5+ | |15x | | | | | |---|---| |---|---| |2- | |2/ | | | | | |---|---|---|---|---|Output
25431 12345 34512 41253 53124Input
5 |---|---|---|---|---| |2- |12+|2 |10x|2/ | | | | | | | | | |---| | | | | |12x| | | | | | | | | |---| | | |---| |3- | | | |20x| | | | | | | | |---| |---| | | |20+| | | | | | | | | | |---| |---| |---| | | | | |-------------------|Output
34251 53412 15324 42135 21543